310801: CF1889F. Doremy's Average Tree

F. Doremy's Average Treetime limit per test3 secondsmemory limit per test1024 megabytesinputstandard inputoutputstandard output

Doremy has a rooted tree of size $n$ whose root is vertex $r$. Initially there is a number $w_i$ written on vertex $i$. Doremy can use her power to perform this operation at most $k$ times:

1. Choose a vertex $x$ ($1 \leq x \leq n$).
2. Let $s = \frac{1}{|T|}\sum_{i \in T} w_i$ where $T$ is the set of all vertices in $x$'s subtree.
3. For all $i \in T$, assign $w_i := s$.

Doremy wants to know what is the lexicographically smallest$^\dagger$ array $w$ after performing all the operations. Can you help her?

If there are multiple answers, you may output any one.

$^\dagger$ For arrays $a$ and $b$ both of length $n$, $a$ is lexicographically smaller than $b$ if and only if there exist an index $i$ ($1 \leq i \le n$) such that $a_i < b_i$ and for all indices $j$ such that $j<i$, $a_j=b_j$ is satisfied.

Input

The input consists of multiple test cases. The first line contains a single integer $t$ ($1\le t\le 10^4$) — the number of test cases. The description of the test cases follows.

The first line contains three integers $n$, $r$, $k$ ($2 \le n \le 5000$, $1 \le r \le n$, $0 \le k \le \min(500,n)$).

The second line contains $n$ integers $w_1,w_2,\ldots,w_n$ ($1 \le w_i \le 10^6$).

Each of the next $n-1$ lines contains two integers $u_i$, $v_i$ ($1 \leq u_i, v_i \leq n$), representing an edge between $u_i$ and $v_i$.

It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $n$ does not exceed $50\,000$.

Output

For each test case, In the first line, output a single integer $cnt$ ($0 \le cnt \le k$) — the number of operations you perform.

Then, in the second line output $cnt$ integers $p_1,p_2,\ldots,p_{cnt}$ — $x$ is chosen to be $p_i$ for $i$-th operation.

If there are multiple answers, you may output any one.

ExampleInput

4
6 1 1
1 9 2 6 1 8
1 2
1 3
2 4
3 6
3 5
7 7 2
3 1 3 3 1 1 2
7 1
7 2
7 4
1 5
2 3
4 6
6 5 1
3 1 3 1 1 3
5 3
5 1
5 6
3 4
1 2
3 2 1
1000000 999999 999997
2 1
1 3

Output

1
2
2
1 4
1
5
1
1

Note

In the first test case:

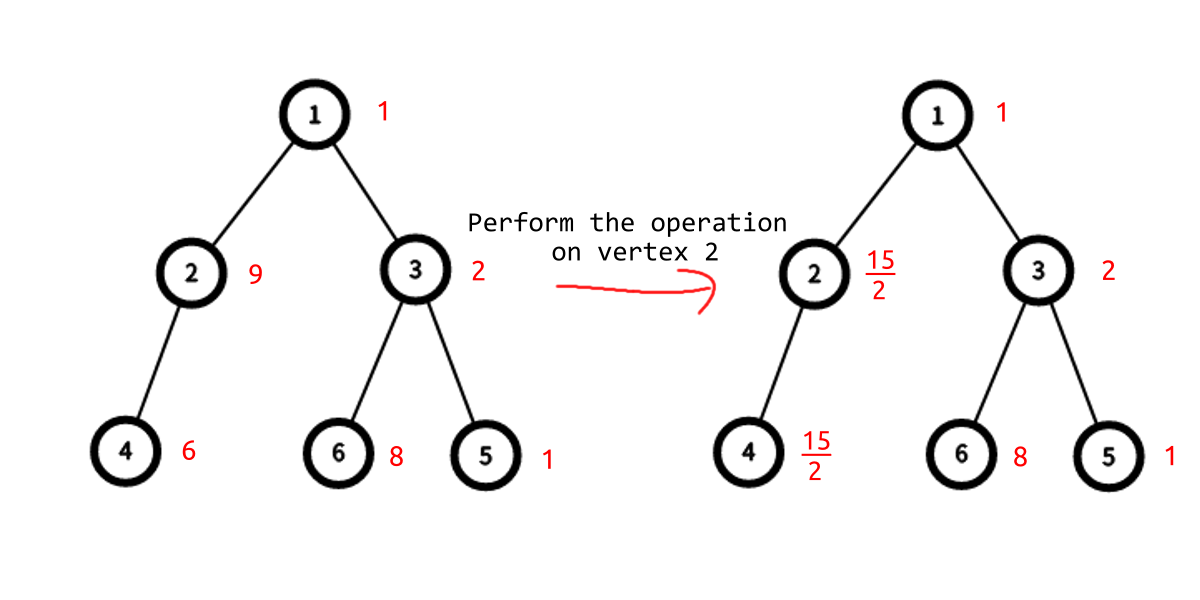
At first $w=[1,9,2,6,1,8]$. You can choose some vertex $x$ to perform at most one operation.

• If $x=1$, $w=[\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2}]$.
• If $x=2$, $w=[1,\frac{15}{2},2,\frac{15}{2},1,8]$.
• If $x=3$, $w=[1,9,\frac{11}{3},6,\frac{11}{3},\frac{11}{3}]$.
• If $x \in \{4, 5, 6\}$, $w=[1,9,2,6,1,8]$.
• If you don't perform any operation, $w=[1,9,2,6,1,8]$.

$w$ is lexicographically smallest when $x=2$.

**题目大意：**

Doremy有一棵大小为n的以r为根的树。最初，顶点i上写有数字w_i。Doremy可以使用她的力量执行以下操作最多k次：

1. 选择一个顶点x（1≤x≤n）。
2. 让s=1/|T| * ∑(i属于T) w_i，其中T是x子树中所有顶点的集合。
3. 对于所有i属于T，赋值w_i:=s。

Doremy想知道执行所有操作后，w数组字典序最小的是什么。你能帮她吗？

如果有多个答案，你可以输出任何一个。

**输入数据格式：**

输入由多个测试用例组成。第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。接下来是测试用例的描述。

每个测试用例的第一行包含三个整数n、r、k（2≤n≤5000，1≤r≤n，0≤k≤min(500,n)）。

第二行包含n个整数w_1,w_2,…,w_n（1≤w_i≤10^6）。

接下来n-1行，每行包含两个整数u_i、v_i（1≤u_i,v_i≤n），表示u_i和v_i之间的边。

保证给定的边构成一棵树。

保证n的总和不超过50,000。

**输出数据格式：**

对于每个测试用例，在第一行输出一个整数cnt（0≤cnt≤k）——你执行的操作数。

然后在第二行输出cnt个整数p_1,p_2,…,p_cnt——第i次操作选择的x是p_i。

如果有多个答案，你可以输出任何一个。

**公式（LaTeX格式）：**

- 平均值计算公式：$$
s = \frac{1}{|T|} \sum_{i \in T} w_i
$$

**注意：**

- 字典序最小：对于长度为n的数组a和b，如果存在一个索引i（1≤i≤n），使得a_i < b_i，并且对于所有索引j（j < i），a_j = b_j，则a在字典序上小于b。**题目大意：** Doremy有一棵大小为n的以r为根的树。最初，顶点i上写有数字w_i。Doremy可以使用她的力量执行以下操作最多k次： 1. 选择一个顶点x（1≤x≤n）。 2. 让s=1/|T| * ∑(i属于T) w_i，其中T是x子树中所有顶点的集合。 3. 对于所有i属于T，赋值w_i:=s。 Doremy想知道执行所有操作后，w数组字典序最小的是什么。你能帮她吗？ 如果有多个答案，你可以输出任何一个。 **输入数据格式：** 输入由多个测试用例组成。第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含三个整数n、r、k（2≤n≤5000，1≤r≤n，0≤k≤min(500,n)）。 第二行包含n个整数w_1,w_2,…,w_n（1≤w_i≤10^6）。 接下来n-1行，每行包含两个整数u_i、v_i（1≤u_i,v_i≤n），表示u_i和v_i之间的边。 保证给定的边构成一棵树。 保证n的总和不超过50,000。 **输出数据格式：** 对于每个测试用例，在第一行输出一个整数cnt（0≤cnt≤k）——你执行的操作数。 然后在第二行输出cnt个整数p_1,p_2,…,p_cnt——第i次操作选择的x是p_i。 如果有多个答案，你可以输出任何一个。 **公式（LaTeX格式）：** - 平均值计算公式：$$ s = \frac{1}{|T|} \sum_{i \in T} w_i $$ **注意：** - 字典序最小：对于长度为n的数组a和b，如果存在一个索引i（1≤i≤n），使得a_i < b_i，并且对于所有索引j（j < i），a_j = b_j，则a在字典序上小于b。