310753: CF1881F. Minimum Maximum Distance
Description
You have a tree with $n$ vertices, some of which are marked. A tree is a connected undirected graph without cycles.
Let $f_i$ denote the maximum distance from vertex $i$ to any of the marked vertices.
Your task is to find the minimum value of $f_i$ among all vertices.
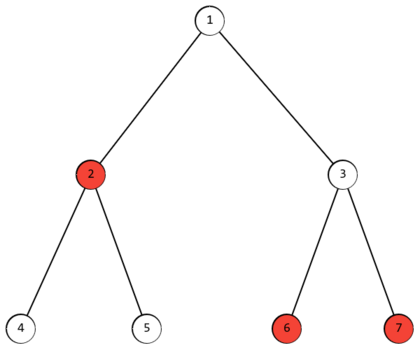
For example, in the tree shown in the example, vertices $2$, $6$, and $7$ are marked. Then the array $f(i) = [2, 3, 2, 4, 4, 3, 3]$. The minimum $f_i$ is for vertices $1$ and $3$.
InputThe first line contains an integer $t$ ($1 \le t \le 10^4$) — the number of test cases.
The first line of each test case contains two integers $n$ and $k$ ($1 \le k \le n \le 2 \cdot 10^5$) — the number of vertices in the tree and the number of marked vertices, respectively.
The second line of each test case contains $k$ integers $a_i$ ($1 \le a_i \le n, a_{i-1} < a_i$) — the indices of the marked vertices.
The next $n - 1$ lines contain two integers $u_i$ and $v_i$ — the indices of vertices connected by the $i$-th edge.
It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.
OutputFor each test case, output a single integer — the minimum value of $f_i$ among all vertices.
ExamplesInput6 7 3 2 6 7 1 2 1 3 2 4 2 5 3 6 3 7 4 4 1 2 3 4 1 2 2 3 3 4 5 1 1 1 2 1 3 1 4 1 5 5 2 4 5 1 2 2 3 1 4 4 5 10 8 1 2 3 4 5 8 9 10 2 10 10 5 5 3 3 1 1 7 7 4 4 9 8 9 6 1 10 9 1 2 4 5 6 7 8 9 10 1 3 3 9 9 4 4 10 10 6 6 7 7 2 2 5 5 8Output
2 2 0 1 4 5Input
3 6 1 3 1 2 1 3 3 4 3 5 2 6 5 3 1 2 5 1 2 1 3 2 4 3 5 7 1 2 3 2 2 6 6 1 5 6 7 6 4 5Output
0 2 0
Output
输入数据格式:
- 第一行包含一个整数t(1≤t≤10^4),表示测试用例的数量。
- 每个测试用例的第一行包含两个整数n和k(1≤k≤n≤2×10^5),分别表示树中顶点的数量和标记顶点的数量。
- 每个测试用例的第二行包含k个整数a_i(1≤a_i≤n,a_{i-1}
- 保证所有测试用例的n之和不超过2×10^5。
输出数据格式:
- 对于每个测试用例,输出一个整数,表示所有顶点中f_i的最小值。
示例输入输出已经给出,可以参考原文档中的Samples部分。题目大意:给定一个有n个顶点的树(树是一个无环的连通无向图),树中的一些顶点被标记。记f_i为顶点i到任意一个标记顶点的最大距离。任务是找到所有顶点中f_i的最小值。 输入数据格式: - 第一行包含一个整数t(1≤t≤10^4),表示测试用例的数量。 - 每个测试用例的第一行包含两个整数n和k(1≤k≤n≤2×10^5),分别表示树中顶点的数量和标记顶点的数量。 - 每个测试用例的第二行包含k个整数a_i(1≤a_i≤n,a_{i-1}