310703: CF1873E. Building an Aquarium

E. Building an Aquariumtime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

You love fish, that's why you have decided to build an aquarium. You have a piece of coral made of $n$ columns, the $i$-th of which is $a_i$ units tall. Afterwards, you will build a tank around the coral as follows:

• Pick an integer $h \geq 1$ — the height of the tank. Build walls of height $h$ on either side of the tank.
• Then, fill the tank up with water so that the height of each column is $h$, unless the coral is taller than $h$; then no water should be added to this column.

For example, with $a=[3,1,2,4,6,2,5]$ and a height of $h=4$, you will end up using a total of $w=8$ units of water, as shown. You can use at most $x$ units of water to fill up the tank, but you want to build the biggest tank possible. What is the largest value of $h$ you can select?Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case contains two positive integers $n$ and $x$ ($1 \leq n \leq 2 \cdot 10^5$; $1 \leq x \leq 10^9$) — the number of columns of the coral and the maximum amount of water you can use.

The second line of each test case contains $n$ space-separated integers $a_i$ ($1 \leq a_i \leq 10^9$) — the heights of the coral.

The sum of $n$ over all test cases doesn't exceed $2 \cdot 10^5$.

Output

For each test case, output a single positive integer $h$ ($h \geq 1$) — the maximum height the tank can have, so you need at most $x$ units of water to fill up the tank.

We have a proof that under these constraints, such a value of $h$ always exists.

ExampleInput

5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1

Output

4
4
2
335
1000000001

Note

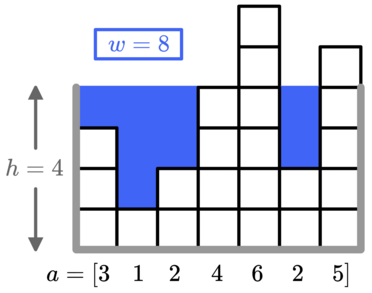
The first test case is pictured in the statement. With $h=4$ we need $8$ units of water, but if $h$ is increased to $5$ we need $13$ units of water, which is more than $x=9$. So $h=4$ is optimal.

In the second test case, we can pick $h=4$ and add $3$ units to each column, using a total of $9$ units of water. It can be shown that this is optimal.

In the third test case, we can pick $h=2$ and use all of our water, so it is optimal.

题目大意：
你打算建造一个养鱼缸，围绕一块由n列珊瑚建造。珊瑚的第i列高a_i单位。按照以下步骤建造鱼缸：
1. 选择一个整数h≥1——鱼缸的高度。在鱼缸两侧建造高度为h的墙。
2. 然后将鱼缸装满水，使每列的高度都是h，除非珊瑚高于h；那么这个柱子就不应该加水。

输入数据格式：
第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。
每个测试用例的第一行包含两个正整数n和x（1≤n≤2*10^5；1≤x≤10^9）——珊瑚的列数和你可以使用的最大水量。
每个测试用例的第二行包含n个空格分隔的整数a_i（1≤a_i≤10^9）——珊瑚的高度。
所有测试用例的n之和不超过2*10^5。

输出数据格式：
对于每个测试用例，输出一个正整数h（h≥1）——鱼缸可以达到的最大高度，以便你最多使用x单位的水来装满鱼缸。

样例输入输出：
输入：
5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1
输出：
4
4
2
335
1000000001

注意：
第一个测试用例在题目描述中有图示。当h=4时，我们需要8单位的水，但如果h增加到5，我们需要13单位的水，这超过了x=9。所以h=4是最优的。
在第二个测试用例中，我们可以选择h=4，并且向每列添加3单位的水，总共使用9单位的水。可以证明这是最优的。
在第三个测试用例中，我们可以选择h=2，并且使用我们所有的水，所以这是最优的。题目大意： 你打算建造一个养鱼缸，围绕一块由n列珊瑚建造。珊瑚的第i列高a_i单位。按照以下步骤建造鱼缸： 1. 选择一个整数h≥1——鱼缸的高度。在鱼缸两侧建造高度为h的墙。 2. 然后将鱼缸装满水，使每列的高度都是h，除非珊瑚高于h；那么这个柱子就不应该加水。 输入数据格式： 第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。 每个测试用例的第一行包含两个正整数n和x（1≤n≤2*10^5；1≤x≤10^9）——珊瑚的列数和你可以使用的最大水量。 每个测试用例的第二行包含n个空格分隔的整数a_i（1≤a_i≤10^9）——珊瑚的高度。 所有测试用例的n之和不超过2*10^5。 输出数据格式： 对于每个测试用例，输出一个正整数h（h≥1）——鱼缸可以达到的最大高度，以便你最多使用x单位的水来装满鱼缸。 样例输入输出： 输入： 5 7 9 3 1 2 4 6 2 5 3 10 1 1 1 4 1 1 4 3 4 6 1984 2 6 5 9 1 8 1 1000000000 1 输出： 4 4 2 335 1000000001 注意： 第一个测试用例在题目描述中有图示。当h=4时，我们需要8单位的水，但如果h增加到5，我们需要13单位的水，这超过了x=9。所以h=4是最优的。 在第二个测试用例中，我们可以选择h=4，并且向每列添加3单位的水，总共使用9单位的水。可以证明这是最优的。 在第三个测试用例中，我们可以选择h=2，并且使用我们所有的水，所以这是最优的。