310683: CF1869F. Flower-like Pseudotree
Description
A pseudotree is a connected graph which has exactly one cycle and no self-loops. Note that a pseudotree may contain multiple-edges. It can be shown that a pseudotree with $n$ vertices always contains $n$ edges.
After deleting all edges on the cycle in the pseudotree, a forest$^{\dagger}$ will be formed. It can be shown that each tree in the forest will contain exactly one vertex which is on cycle before removing the edges. If all trees in the forest have the same depth$^{\ddagger}$ when picking the vertex on cycle as root, we call the original pseudotree flower-like.
Our friend sszcdjr, had a flower-like pseudotree with $n$ vertices and $n$ edges. However, he forgot all the edges in the pseudotree. Fortunately, he still remembers the degrees of vertices. Specifically, the degree of the $i$-th vertex is $d_i$.
You have to help sszcdjr construct a possible flower-like pseudotree with $n$ vertices, where the degree of the $i$-th vertex is exactly $d_i$, or tell him that it is impossible.
$^{\dagger}$ A forest is a graph in which all connectivity components are trees. A connected graph without cycles and self-loops is called a tree.
$^{\ddagger}$ The depth of a tree with a root is the maximum distance from the root to the vertex of this tree.
InputThe first line of the input contains a single integer $t$ ($1\leq t\leq 10^5$) — the number of test cases. The description of test cases follows.
The first line of each test case contains a single integer $n$ ($2\leq n\leq 10^6$) — the number of vertices.
The second line of each test case contains $n$ integers $d_1,d_2,\ldots,d_n$ ($1\leq d_i\leq n$) — the degree of each vertex.
It is guaranteed that the sum of $n$ over all test cases does not exceed $10^6$.
OutputFor each test case, if there exist a possible flower-like pseudotree:
- Print "Yes" (without quotes) in the first line.
- Then, output $n$ lines, in each line print two integers $u_i$ and $v_i$ — the two vertices that the $i$-th edge connects.
If there are multiple answers, you may output any of them.
Otherwise, print "No" (without quotes) in the only line of output.
You can output the first line of each test case in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.
ExampleInput6 3 2 2 2 4 1 2 3 4 7 4 3 3 1 1 1 1 6 1 1 2 2 3 3 10 1 1 5 2 1 1 1 1 1 6 9 1 1 3 1 1 4 1 1 5Output
Yes 1 2 2 3 3 1 No Yes 1 2 2 3 3 1 1 4 1 5 2 6 3 7 Yes 5 6 6 5 1 3 2 4 3 5 4 6 No Yes 3 6 6 9 9 3 1 3 2 6 4 6 5 9 7 9 8 9Note
In the first test case, the only possible flower-like psuedotree is:
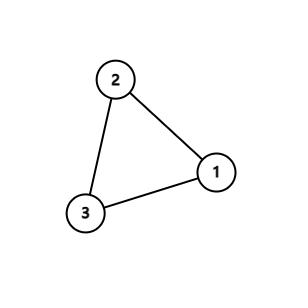
After deleting all edges on the cycle in the pseudotree, each tree has depth $0$.
In the second test case, it can be proven that there's no such flower-like psuedotree.
In the third test case, one of the possible flower-like psuedotrees is:
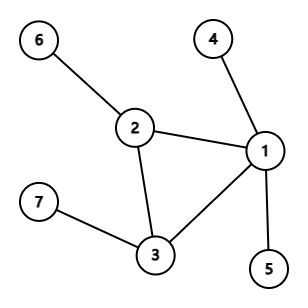
Output
一个**伪树**是一个连通图,它恰好有一个环且没有自环。注意,伪树可能包含多条边。可以证明,一个有n个顶点的伪树总是包含n条边。
在删除伪树中环上的所有边后,将形成一个森林。可以证明,森林中的每棵树都恰好包含一个在删除边之前在环上的顶点。如果森林中的所有树在选择环上的顶点作为根时具有相同的深度,我们称原始伪树为**花形**。
我们的朋友sszcdjr有一个有n个顶点和n条边的花形伪树。然而,他忘记了伪树中的所有边。幸运的是,他还记得顶点的度数。具体来说,第i个顶点的度数是d_i。
你必须帮助sszcdjr构建一个可能的花形伪树,其中有n个顶点,其中第i个顶点的度数恰好是d_i,或者告诉他这是不可能的。
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。
- 每个测试用例的第一行包含一个整数n(2≤n≤10^6)——顶点的数量。
- 每个测试用例的第二行包含n个整数d_1,d_2,…,d_n(1≤d_i≤n)——每个顶点的度数。
- 保证所有测试用例的n之和不超过10^6。
输出:
- 对于每个测试用例,如果存在可能的花形伪树:
- 在第一行打印"Yes"(不带引号)。
- 然后,输出n行,每行打印两个整数u_i和v_i——第i条边连接的两个顶点。
- 如果有多个答案,你可以输出其中任何一个。
- 否则,在唯一的输出行中打印"No"(不带引号)。
- 你可以以任何情况(大写或小写)输出每个测试用例的第一行。例如,字符串"yEs"、"yes"、"Yes"和"YES"将被识别为积极响应。题目大意: 一个**伪树**是一个连通图,它恰好有一个环且没有自环。注意,伪树可能包含多条边。可以证明,一个有n个顶点的伪树总是包含n条边。 在删除伪树中环上的所有边后,将形成一个森林。可以证明,森林中的每棵树都恰好包含一个在删除边之前在环上的顶点。如果森林中的所有树在选择环上的顶点作为根时具有相同的深度,我们称原始伪树为**花形**。 我们的朋友sszcdjr有一个有n个顶点和n条边的花形伪树。然而,他忘记了伪树中的所有边。幸运的是,他还记得顶点的度数。具体来说,第i个顶点的度数是d_i。 你必须帮助sszcdjr构建一个可能的花形伪树,其中有n个顶点,其中第i个顶点的度数恰好是d_i,或者告诉他这是不可能的。 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。 - 每个测试用例的第一行包含一个整数n(2≤n≤10^6)——顶点的数量。 - 每个测试用例的第二行包含n个整数d_1,d_2,…,d_n(1≤d_i≤n)——每个顶点的度数。 - 保证所有测试用例的n之和不超过10^6。 输出: - 对于每个测试用例,如果存在可能的花形伪树: - 在第一行打印"Yes"(不带引号)。 - 然后,输出n行,每行打印两个整数u_i和v_i——第i条边连接的两个顶点。 - 如果有多个答案,你可以输出其中任何一个。 - 否则,在唯一的输出行中打印"No"(不带引号)。 - 你可以以任何情况(大写或小写)输出每个测试用例的第一行。例如,字符串"yEs"、"yes"、"Yes"和"YES"将被识别为积极响应。