310678: CF1869B. 2D Traveling

B. 2D Travelingtime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Piggy lives on an infinite plane with the Cartesian coordinate system on it.

There are $n$ cities on the plane, numbered from $1$ to $n$, and the first $k$ cities are defined as major cities. The coordinates of the $i$-th city are $(x_i,y_i)$.

Piggy, as a well-experienced traveller, wants to have a relaxing trip after Zhongkao examination. Currently, he is in city $a$, and he wants to travel to city $b$ by air. You can fly between any two cities, and you can visit several cities in any order while travelling, but the final destination must be city $b$.

Because of active trade between major cities, it's possible to travel by plane between them for free. Formally, the price of an air ticket $f(i,j)$ between two cities $i$ and $j$ is defined as follows:

$$ f(i,j)= \begin{cases} 0, & \text{if cities }i \text{ and }j \text{ are both major cities} \\ |x_i-x_j|+|y_i-y_j|, & \text{otherwise} \end{cases} $$

Piggy doesn't want to save time, but he wants to save money. So you need to tell him the minimum value of the total cost of all air tickets if he can take any number of flights.

Input

The first line of input contains a single integer $t$ ($1\le t\le 10^4$) — the number of test cases. The description of test cases follows.

The first line of each test case contains four integers $n$, $k$, $a$ and $b$ ($2\le n\le 2\cdot 10^5$, $0\le k\le n$, $1\le a,b\le n$, $a\ne b$) — the number of cities, the number of major cities and the numbers of the starting and the ending cities.

Then $n$ lines follow, the $i$-th line contains two integers $x_i$ and $y_i$ ($-10^9\le x_i,y_i\le 10^9$) — the coordinates of the $i$-th city. The first $k$ lines describe major cities. It is guaranteed that all coordinates are pairwise distinct.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2\cdot 10^5$.

Output

For each test case, print a single integer — the minimum value of the total price of all air tickets.

ExampleInput

5
6 2 3 5
0 0
1 -2
-2 1
-1 3
2 -2
-3 -3
2 0 1 2
-1000000000 -1000000000
1000000000 1000000000
7 5 4 2
154 147
-154 -147
123 456
20 23
43 20
998 244
353 100
3 1 3 1
0 10
1 20
2 30
4 3 2 4
0 0
-100 100
-1 -1
-1 0

Output

4
4000000000
0
22
1

Note

In the first test case:

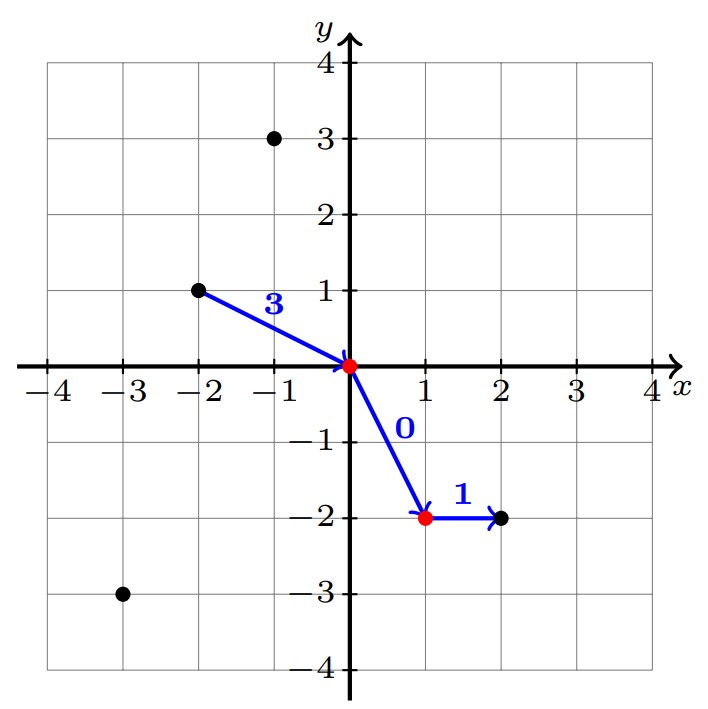The major cities are marked red.

The optimal way to choose the flights is: $3\rightarrow 1 \rightarrow 2 \rightarrow 5$, which will cost $3+0+1=4$. Note that the flight $1\rightarrow 2$ costs $0$, because both city $1$ and $2$ are major cities.

In the second test case, since there are only $2$ cities, the only way is to take a flight from city $1$ to $2$.

In the third test case, since city $2$ and $4$ are both major cities, Piggy can directly take a flight from city $2$ to $4$, which costs $0$.

In the fourth test case, Piggy can choose to take the following flights: $3\rightarrow 2\rightarrow 1$, and the cost is $11+11=22$.

题目大意：
Piggy生活在一个带有笛卡尔坐标系的无限平面上。平面上有n个城市，编号从1到n，其中前k个城市被定义为大城市。第i个城市的坐标是(xi,yi)。Piggy想要在高考后进行一次放松的旅行，他目前在城市a，想要通过飞行旅行到城市b。他可以在任意两个城市之间飞行，旅行中可以按任意顺序访问几个城市，但最终目的地必须是城市b。由于大城市之间的活跃贸易，可以免费在大城市之间飞行。机票的价格f(i,j)定义如下：

f(i,j)=
0, 如果城市i和j都是大城市
|x_i-x_j|+|y_i-y_j|, 否则

Piggy不想节省时间，只想节省钱。所以他需要知道如果他能乘坐任意数量的航班，所有机票的总费用的最小值是多少。

输入输出数据格式：
输入描述：
第一行包含一个整数t（1≤t≤10^4），表示测试用例的数量。接下来是每个测试用例的描述。
每个测试用例的第一行包含四个整数n、k、a和b（2≤n≤2*10^5，0≤k≤n，1≤a,b≤n，a≠b），分别表示城市的数量、大城市的数量以及起始城市和结束城市的编号。
然后是n行，每行包含两个整数xi和yi（-10^9≤xi,yi≤10^9），表示第i个城市的坐标。前k行描述大城市。保证所有坐标都是两两不同的。
保证所有测试用例的n之和不超过2*10^5。

输出描述：
对于每个测试用例，输出一个整数，表示所有机票的总费用的最小值。题目大意： Piggy生活在一个带有笛卡尔坐标系的无限平面上。平面上有n个城市，编号从1到n，其中前k个城市被定义为大城市。第i个城市的坐标是(xi,yi)。Piggy想要在高考后进行一次放松的旅行，他目前在城市a，想要通过飞行旅行到城市b。他可以在任意两个城市之间飞行，旅行中可以按任意顺序访问几个城市，但最终目的地必须是城市b。由于大城市之间的活跃贸易，可以免费在大城市之间飞行。机票的价格f(i,j)定义如下： f(i,j)= 0, 如果城市i和j都是大城市 |x_i-x_j|+|y_i-y_j|, 否则 Piggy不想节省时间，只想节省钱。所以他需要知道如果他能乘坐任意数量的航班，所有机票的总费用的最小值是多少。 输入输出数据格式： 输入描述： 第一行包含一个整数t（1≤t≤10^4），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含四个整数n、k、a和b（2≤n≤2*10^5，0≤k≤n，1≤a,b≤n，a≠b），分别表示城市的数量、大城市的数量以及起始城市和结束城市的编号。 然后是n行，每行包含两个整数xi和yi（-10^9≤xi,yi≤10^9），表示第i个城市的坐标。前k行描述大城市。保证所有坐标都是两两不同的。 保证所有测试用例的n之和不超过2*10^5。 输出描述： 对于每个测试用例，输出一个整数，表示所有机票的总费用的最小值。