310593: CF1856E2. PermuTree (hard version)
Description
This is the hard version of the problem. The differences between the two versions are the constraint on $n$ and the time limit. You can make hacks only if both versions of the problem are solved.
You are given a tree with $n$ vertices rooted at vertex $1$.
For some permutation$^\dagger$ $a$ of length $n$, let $f(a)$ be the number of pairs of vertices $(u, v)$ such that $a_u < a_{\operatorname{lca}(u, v)} < a_v$. Here, $\operatorname{lca}(u,v)$ denotes the lowest common ancestor of vertices $u$ and $v$.
Find the maximum possible value of $f(a)$ over all permutations $a$ of length $n$.
$^\dagger$ A permutation of length $n$ is an array consisting of $n$ distinct integers from $1$ to $n$ in arbitrary order. For example, $[2,3,1,5,4]$ is a permutation, but $[1,2,2]$ is not a permutation ($2$ appears twice in the array), and $[1,3,4]$ is also not a permutation ($n=3$ but there is $4$ in the array).
InputThe first line contains a single integer $n$ ($2 \le n \le 10^6$).
The second line contains $n - 1$ integers $p_2,p_3,\ldots,p_n$ ($1 \le p_i < i$) indicating that there is an edge between vertices $i$ and $p_i$.
OutputOutput the maximum value of $f(a)$.
ExamplesInput5 1 1 3 3Output
4Input
2 1Output
0Input
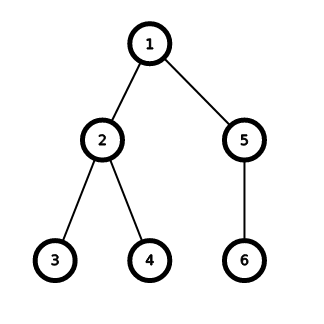
6 1 2 2 1 5Output
7Input
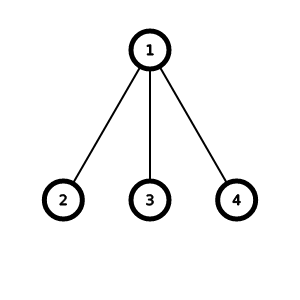
4 1 1 1Output
2Note
The tree in the first test:
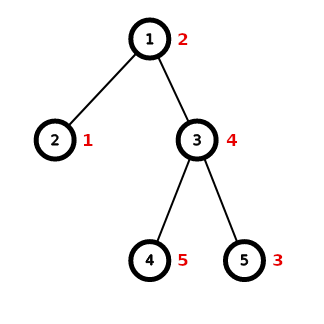
One possible optimal permutation $a$ is $[2, 1, 4, 5, 3]$ with $4$ suitable pairs of vertices:
- $(2, 3)$, since $\operatorname{lca}(2, 3) = 1$ and $1 < 2 < 4$,
- $(2, 4)$, since $\operatorname{lca}(2, 4) = 1$ and $1 < 2 < 5$,
- $(2, 5)$, since $\operatorname{lca}(2, 5) = 1$ and $1 < 2 < 3$,
- $(5, 4)$, since $\operatorname{lca}(5, 4) = 3$ and $3 < 4 < 5$.
The tree in the third test:
The tree in the fourth test:
Output
输入数据格式:第一行包含一个整数n(2≤n≤10^6)。第二行包含n-1个整数p2,p3,…,pn(1≤pi
输出数据格式:输出f(a)的最大值。
注意:排列a是包含n个不同的从1到n的整数的数组,数组中的数字可以任意排列。例如,[2,3,1,5,4]是一个排列,但[1,2,2]不是排列(数组中2出现了两次),[1,3,4]也不是排列(n=3,但数组中有4)。题目大意:给定一棵有n个顶点的树,根节点为1。对于长度为n的某个排列a,定义f(a)为满足au < a_{lca}(u, v) < av的顶点对(u, v)的数量。这里,lca(u,v)表示顶点u和v的最低公共祖先。求所有长度为n的排列a中f(a)的最大可能值。 输入数据格式:第一行包含一个整数n(2≤n≤10^6)。第二行包含n-1个整数p2,p3,…,pn(1≤pi