310551: CF1850E. Cardboard for Pictures
Description
Mircea has $n$ pictures. The $i$-th picture is a square with a side length of $s_i$ centimeters.
He mounted each picture on a square piece of cardboard so that each picture has a border of $w$ centimeters of cardboard on all sides. In total, he used $c$ square centimeters of cardboard. Given the picture sizes and the value $c$, can you find the value of $w$?
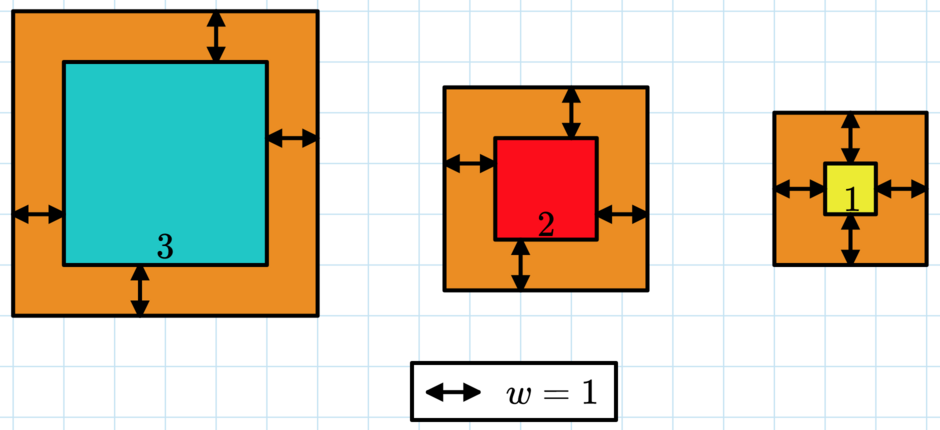A picture of the first test case. Here $c = 50 = 5^2 + 4^2 + 3^2$, so $w=1$ is the answer. Please note that the piece of cardboard goes behind each picture, not just the border.
InputThe first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.
The first line of each test case contains two positive integers $n$ ($1 \leq n \leq 2 \cdot 10^5$) and $c$ ($1 \leq c \leq 10^{18}$) — the number of paintings, and the amount of used square centimeters of cardboard.
The second line of each test case contains $n$ space-separated integers $s_i$ ($1 \leq s_i \leq 10^4$) — the sizes of the paintings.
The sum of $n$ over all test cases doesn't exceed $2 \cdot 10^5$.
Additional constraint on the input: Such an integer $w$ exists for each test case.
Please note, that some of the input for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).
OutputFor each test case, output a single integer — the value of $w$ ($w \geq 1$) which was used to use exactly $c$ squared centimeters of cardboard.
ExampleInput10 3 50 3 2 1 1 100 6 5 500 2 2 2 2 2 2 365 3 4 2 469077255466389 10000 2023 10 635472106413848880 9181 4243 7777 1859 2017 4397 14 9390 2245 7225 7 176345687772781240 9202 9407 9229 6257 7743 5738 7966 14 865563946464579627 3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384 19 977162053008871403 9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161 18 886531871815571953 2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764Output
1 2 4 5 7654321 126040443 79356352 124321725 113385729 110961227Note
The first test case is explained in the statement.
For the second test case, the chosen $w$ was $2$, thus the only cardboard covers an area of $c = (2 \cdot 2 + 6)^2 = 10^2 = 100$ squared centimeters.
For the third test case, the chosen $w$ was $4$, which obtains the covered area $c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$ squared centimeters.
Input
题意翻译
# 题目描述 Mircea有n张照片。第i张照片是一个边长为si厘米的正方形。 他将每张照片装在一个正方形的纸板上，使得每张照片的四周都有w厘米的纸板边框。总共，他使用了c平方厘米的纸板。根据照片的尺寸和c的值，你能找出w的值吗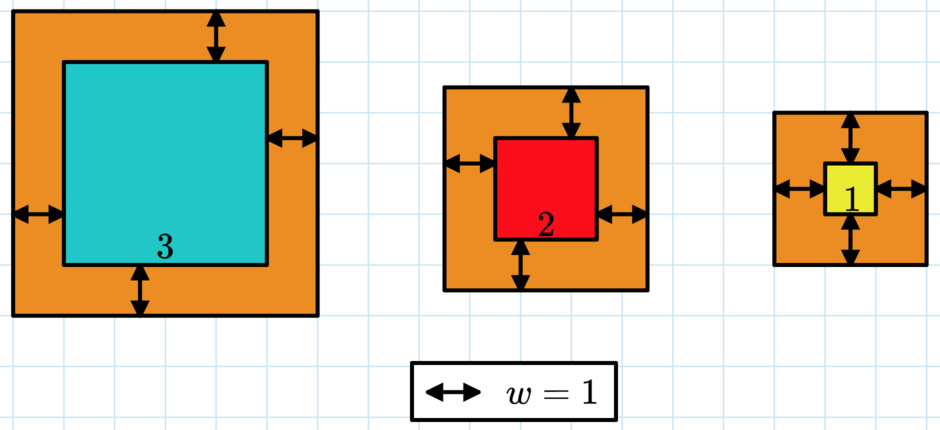？  c=50=5²+4²+3²，所以w = 1 是本题目的答案。请注意，纸板的一角会出现在每张图片的后面，而不仅仅是边框上。 # 输入格式 输入的第一行包含一个整数t（1≤t≤1000），表示测试用例的数量。 每个测试用例的第一行包含两个正整数n（1≤n≤2⋅105）和c（1≤c≤1018），分别表示照片的数量和使用的卡纸的面积。 每个测试用例的第二行包含n个空格分隔的整数si（1≤si≤104），表示每张照片的尺寸。 所有测试用例中n的总和不超过2⋅105。 输入的附加约束条件：对于每个测试用例，存在一个整数w。 请注意，一些测试用例中的输入可能超过32位整数的范围，因此您应该在编程语言中至少使用64位整数类型（如C++中的long long类型）。 # 输出格式 对于每个测试用例，输出一个整数，表示使用了多少宽度的边框w，使得其恰好使用了c平方厘米的纸板。 # 样例 ``` 输入：10 3 50 3 2 1 1 100 6 5 500 2 2 2 2 2 2 365 3 4 2 469077255466389 10000 2023 10 635472106413848880 9181 4243 7777 1859 2017 4397 14 9390 2245 7225 7 176345687772781240 9202 9407 9229 6257 7743 5738 7966 14 865563946464579627 3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384 19 977162053008871403 9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161 18 886531871815571953 2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764 ``` ``` 输出：1 2 4 5 7654321 126040443 79356352 124321725 113385729 110961227 # 说明以及提示 ``` 在第一个测试用例中，根据题目给出的例子 ``` 我们需要使用1张照片，因此可以选择任意宽度的边框w。 在第二个测试用例中，假设我们选择的宽度w为22，那么每张照片需要的纸板面积为(2w+6)^2=10^2=100平方厘米。 ``` 在第三个测试用例中，假设我们选择的宽度w为44，那么每张照片需要的纸板面积为 ``` (2w+2)^2×5=10^2×5=100×5=500平方厘米。Output
Mircea有n张图片，每张图片是一个边长为s_i厘米的正方形。他将每张图片贴在一个正方形的纸板上，使得每张图片四周都有w厘米的纸板边框。总共使用了c平方厘米的纸板。给定图片的大小和c的值，你能找到w的值吗？
输入数据格式：
第一行包含一个整数t（1≤t≤1000）——测试用例的数量。
每个测试用例的第一行包含两个正整数n（1≤n≤2×10^5）和c（1≤c≤10^18）——图片的数量和使用的平方厘米的纸板数量。
每个测试用例的第二行包含n个空格分隔的整数s_i（1≤s_i≤10^4）——图片的大小。
所有测试用例的n之和不超过2×10^5。
输入数据的一个额外限制：对于每个测试用例，都存在一个整数w。
输出数据格式：
对于每个测试用例，输出一个整数——使用的w（w≥1）的值，以恰好使用c平方厘米的纸板。题目大意： Mircea有n张图片，每张图片是一个边长为s_i厘米的正方形。他将每张图片贴在一个正方形的纸板上，使得每张图片四周都有w厘米的纸板边框。总共使用了c平方厘米的纸板。给定图片的大小和c的值，你能找到w的值吗？ 输入数据格式： 第一行包含一个整数t（1≤t≤1000）——测试用例的数量。 每个测试用例的第一行包含两个正整数n（1≤n≤2×10^5）和c（1≤c≤10^18）——图片的数量和使用的平方厘米的纸板数量。 每个测试用例的第二行包含n个空格分隔的整数s_i（1≤s_i≤10^4）——图片的大小。 所有测试用例的n之和不超过2×10^5。 输入数据的一个额外限制：对于每个测试用例，都存在一个整数w。 输出数据格式： 对于每个测试用例，输出一个整数——使用的w（w≥1）的值，以恰好使用c平方厘米的纸板。