310467: CF1838C. No Prime Differences

C. No Prime Differencestime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

You are given integers $n$ and $m$. Fill an $n$ by $m$ grid with the integers $1$ through $n\cdot m$, in such a way that for any two adjacent cells in the grid, the absolute difference of the values in those cells is not a prime number. Two cells in the grid are considered adjacent if they share a side.

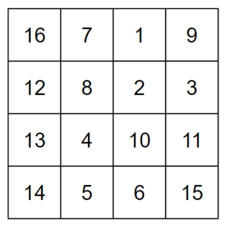
It can be shown that under the given constraints, there is always a solution.

Input

The first line of the input contains a single integer $t$ ($1 \le t \le 1000$) — the number of test cases. The description of the test cases follows.

The first and only line of each test case contains two integers $n$ and $m$ ($4 \le n, m \le 1000$) — the dimensions of the grid.

It is guaranteed that the sum of $n\cdot m$ over all test cases does not exceed $10^6$.

Output

For each test case, output $n$ lines of $m$ integers each, representing the final grid. Every number from $1$ to $n\cdot m$ should appear exactly once in the grid.

The extra spaces and blank lines in the sample output below are only present to make the output easier to read, and are not required.

If there are multiple solutions, print any of them.

ExampleInput

3
4 4
5 7
6 4

Output

16  7  1  9
12  8  2  3
13  4 10 11
14  5  6 15

29 23 17  9  5  6  2
33 27 21 15 11  7  1
32 31 25 19 20 16 10
26 30 24 18 14  8  4
35 34 28 22 13 12  3

 2  3  7 11
 8  9  1 10
17 13  5  4
18 14  6 12
19 23 15 21
20 24 16 22

Note

The first sample case corresponds to the picture above. The only absolute differences between adjacent elements in this grid are $1$, $4$, $6$, $8$, and $9$, none of which are prime.

题目大意：
给定整数n和m，填充一个n*m的网格，网格中的整数从1到n*m，使得网格中任意两个相邻单元格的值的绝对差不是一个素数。两个单元格被认为是相邻的，如果它们共享一个边。

输入数据格式：
第一行包含一个整数t（1≤t≤1000）——测试用例的数量。接下来是t个测试用例的描述。
每个测试用例的第一行包含两个整数n和m（4≤n，m≤1000）——网格的维度。
保证所有测试用例的n*m之和不超过10^6。

输出数据格式：
对于每个测试用例，输出n行，每行m个整数，表示最终的网格。网格中应该恰好出现从1到n*m的每个数字一次。
如果有多个解决方案，输出其中任何一个。

示例输入：
```
3
4 4
5 7
6 4
```

示例输出：
```
16 7 1 9
12 8 2 3
13 4 10 11
14 5 6 15

29 23 17 9 5 6 2
33 27 21 15 11 7 1
32 31 25 19 20 16 10
26 30 24 18 14 8 4
35 34 28 22 13 12 3

2 3 7 11
8 9 1 10
17 13 5 4
18 14 6 12
19 23 15 21
20 24 16 22
```题目大意： 给定整数n和m，填充一个n*m的网格，网格中的整数从1到n*m，使得网格中任意两个相邻单元格的值的绝对差不是一个素数。两个单元格被认为是相邻的，如果它们共享一个边。 输入数据格式： 第一行包含一个整数t（1≤t≤1000）——测试用例的数量。接下来是t个测试用例的描述。 每个测试用例的第一行包含两个整数n和m（4≤n，m≤1000）——网格的维度。 保证所有测试用例的n*m之和不超过10^6。 输出数据格式： 对于每个测试用例，输出n行，每行m个整数，表示最终的网格。网格中应该恰好出现从1到n*m的每个数字一次。 如果有多个解决方案，输出其中任何一个。 示例输入： ``` 3 4 4 5 7 6 4 ``` 示例输出： ``` 16 7 1 9 12 8 2 3 13 4 10 11 14 5 6 15 29 23 17 9 5 6 2 33 27 21 15 11 7 1 32 31 25 19 20 16 10 26 30 24 18 14 8 4 35 34 28 22 13 12 3 2 3 7 11 8 9 1 10 17 13 5 4 18 14 6 12 19 23 15 21 20 24 16 22 ```