310463: CF1837E. Playoff Fixing

E. Playoff Fixingtime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

$2^k$ teams participate in a playoff tournament. The teams are numbered from $1$ to $2^k$, in order of decreasing strength. So, team $1$ is the strongest one, team $2^k$ is the weakest one. A team with a smaller number always defeats a team with a larger number.

First of all, the teams are arranged in some order during a procedure called seeding. Each team is assigned another unique value from $1$ to $2^k$, called a seed, that represents its starting position in the playoff.

The tournament consists of $2^k - 1$ games. They are held as follows: the teams are split into pairs: team with seed $1$ plays against team with seed $2$, team with seed $3$ plays against team with seed $4$ (exactly in this order), and so on (so, $2^{k-1}$ games are played in that phase). When a team loses a game, it is eliminated.

After that, only $2^{k-1}$ teams remain. If only one team remains, it is declared the champion; otherwise, $2^{k-2}$ games are played: in the first one of them, the winner of the game "seed $1$ vs seed $2$" plays against the winner of the game "seed $3$ vs seed $4$", then the winner of the game "seed $5$ vs seed $6$" plays against the winner of the game "seed $7$ vs seed $8$", and so on. This process repeats until only one team remains.

After the tournament ends, the teams are assigned places according to the tournament phase when they were eliminated. In particular:

• the winner of the tournament gets place $1$;
• the team eliminated in the finals gets place $2$;
• both teams eliminated in the semifinals get place $3$;
• all teams eliminated in the quarterfinals get place $5$;
• all teams eliminated in the 1/8 finals get place $9$, and so on.

Now that we established the rules, we do a little rigging. In particular, we want:

• team $1$ (not team with seed $1$) to take place $1$;
• team $2$ to take place $2$;
• teams $3$ and $4$ to take place $3$;
• teams from $5$ to $8$ to take place $5$, and so on.

For example, this picture describes one of the possible ways the tournament can go with $k = 3$, and the resulting places of the teams:

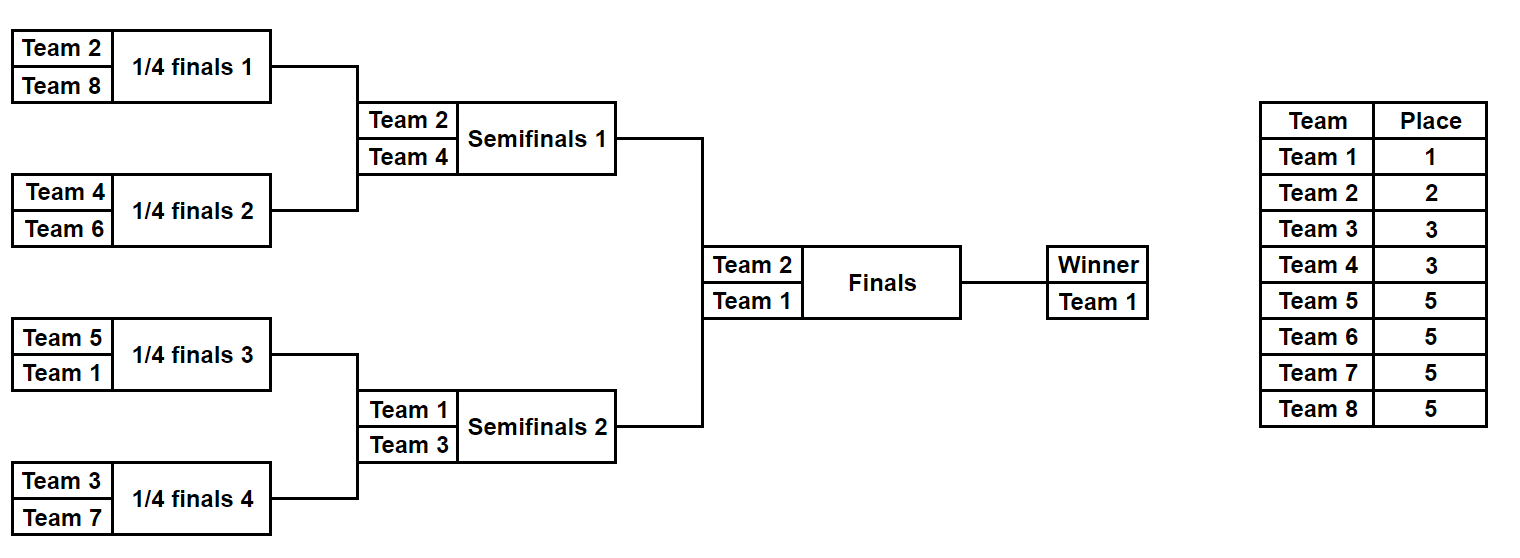
Some seeds are already reserved for some teams (we are not the only ones rigging the tournament, apparently). We have to fill the rest of the seeds with the remaining teams to achieve the desired placements. How many ways are there to do that? Since that value might be large, print it modulo $998\,244\,353$.

Input

The first line contains a single integer $k$ ($0 \le k \le 19$) — there are $2^k$ teams.

The second line contains $2^k$ integers $a_1, a_2, \dots, a_{2^k}$ ($a_i = -1$ or $1 \le a_i \le 2^k$). If $a_i \ne -1$, then team $a_i$ has seed $i$. Otherwise, the seed $i$ is not reserved for any team.

All values, that are not $-1$, are distinct.

Output

Print a single integer — the number of ways to fill the non-reserved seeds so that the tournament goes as planned, modulo $998\,244\,353$.

ExamplesInput

2
1 2 3 4

Output

0

Input

2
1 3 4 2

Output

1

Input

1
-1 -1

Output

2

Input

2
-1 -1 -1 -1

Output

16

Input

3
-1 -1 -1 -1 2 -1 -1 -1

Output

768

Input

0
1

Output

1

题目大意：
在一个季后赛中，共有 \(2^k\) 支队伍参加，队伍从1到\(2^k\)编号，编号越小实力越强。首先进行种子排位，每个队伍被分配一个从1到\(2^k\)的唯一种子值，代表其季后赛的起始位置。比赛分为\(2^k - 1\)场，队伍按种子值配对进行比赛，输掉比赛的队伍被淘汰。比赛分为多个阶段，直到只剩下一支队伍为止。比赛结束后，根据队伍被淘汰的阶段分配名次。

现在要求作弊，使得：
- 第1支队伍（不是种子1）获得第1名；
- 第2支队伍获得第2名；
- 第3和第4支队伍获得第3名；
- 第5到第8支队伍获得第5名，以此类推。

给出已经部分确定的种子分配，求满足上述要求的种子分配方案数，结果模 \(998,244,353\)。

输入输出数据格式：
输入：
- 第一行包含一个整数 \(k\)（\(0 \le k \le 19\)），表示有 \(2^k\) 支队伍。
- 第二行包含 \(2^k\) 个整数 \(a_1, a_2, \dots, a_{2^k}\)，每个整数 \(a_i\) 为 -1 或 \(1 \le a_i \le 2^k\)。如果 \(a_i \ne -1\)，则表示队伍 \(a_i\) 的种子是 \(i\)；如果 \(a_i = -1\)，则表示种子 \(i\) 尚未分配。所有非 -1 的值都是不同的。

输出：
- 输出一个整数，表示满足条件的种子分配方案数，模 \(998,244,353\)。题目大意： 在一个季后赛中，共有 \(2^k\) 支队伍参加，队伍从1到\(2^k\)编号，编号越小实力越强。首先进行种子排位，每个队伍被分配一个从1到\(2^k\)的唯一种子值，代表其季后赛的起始位置。比赛分为\(2^k - 1\)场，队伍按种子值配对进行比赛，输掉比赛的队伍被淘汰。比赛分为多个阶段，直到只剩下一支队伍为止。比赛结束后，根据队伍被淘汰的阶段分配名次。 现在要求作弊，使得： - 第1支队伍（不是种子1）获得第1名； - 第2支队伍获得第2名； - 第3和第4支队伍获得第3名； - 第5到第8支队伍获得第5名，以此类推。 给出已经部分确定的种子分配，求满足上述要求的种子分配方案数，结果模 \(998,244,353\)。 输入输出数据格式： 输入： - 第一行包含一个整数 \(k\)（\(0 \le k \le 19\)），表示有 \(2^k\) 支队伍。 - 第二行包含 \(2^k\) 个整数 \(a_1, a_2, \dots, a_{2^k}\)，每个整数 \(a_i\) 为 -1 或 \(1 \le a_i \le 2^k\)。如果 \(a_i \ne -1\)，则表示队伍 \(a_i\) 的种子是 \(i\)；如果 \(a_i = -1\)，则表示种子 \(i\) 尚未分配。所有非 -1 的值都是不同的。 输出： - 输出一个整数，表示满足条件的种子分配方案数，模 \(998,244,353\)。