310423: CF1831C. Copil Copac Draws Trees
Description
Copil Copac is given a list of $n-1$ edges describing a tree of $n$ vertices. He decides to draw it using the following algorithm:
- Step $0$: Draws the first vertex (vertex $1$). Go to step $1$.
- Step $1$: For every edge in the input, in order: if the edge connects an already drawn vertex $u$ to an undrawn vertex $v$, he will draw the undrawn vertex $v$ and the edge. After checking every edge, go to step $2$.
- Step $2$: If all the vertices are drawn, terminate the algorithm. Else, go to step $1$.
The number of readings is defined as the number of times Copil Copac performs step $1$.
Find the number of readings needed by Copil Copac to draw the tree.
InputEach test contains multiple test cases. The first line of input contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases. The description of test cases follows.
The first line of each test case contains a single integer $n$ ($2 \le n \le 2 \cdot 10^5$) — the number of vertices of the tree.
The following $n - 1$ lines of each test case contain two integers $u_i$ and $v_i$ ($1 \le u_i, v_i \le n$, $u_i \neq v_i$) — indicating that $(u_i,v_i)$ is the $i$-th edge in the list. It is guaranteed that the given edges form a tree.
It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.
OutputFor each test case, output the number of readings Copil Copac needs to draw the tree.
ExampleInput2 6 4 5 1 3 1 2 3 4 1 6 7 5 6 2 4 2 7 1 3 1 2 4 5Output
2 3Note
In the first test case:
After the first reading, the tree will look like this:
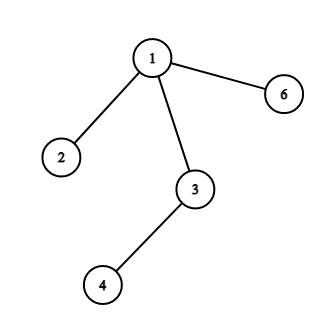
After the second reading:
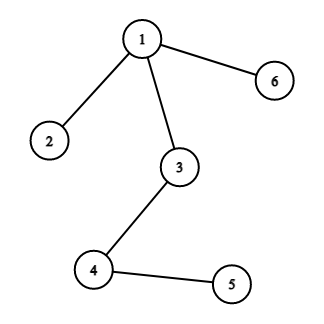
Therefore, Copil Copac needs $2$ readings to draw the tree.
Input
Output
给定一棵树的n-1条边,这棵树有n个顶点。Copil Copac按照以下算法绘制这棵树:
- 步骤0:绘制第一个顶点(顶点1),然后转到步骤1。
- 步骤1:按输入顺序检查每条边。如果边连接已经绘制过的顶点u和未绘制的顶点v,Copil Copac将绘制未绘制的顶点v和这条边。检查完每条边后,转到步骤2。
- 步骤2:如果所有顶点都已绘制,则终止算法。否则,转到步骤1。
读取次数定义为Copil Copac执行步骤1的次数。
求Copil Copac绘制整棵树需要的读取次数。
**输入数据格式:**
每个测试包含多个测试用例。第一行输入包含一个整数t(1≤t≤10^4)——测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数n(2≤n≤2×10^5)——树的顶点数量。
接下来每个测试用例包含n-1行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示(u_i,v_i)是列表中的第i条边。保证给定的边构成一棵树。
保证所有测试用例的n之和不超过2×10^5。
**输出数据格式:**
对于每个测试用例,输出Copil Copac绘制树需要的读取次数。
**示例:**
**输入:**
```
2
6
4 5
1 3
1 2
3 4
1 6
7
5 6
2 4
2 7
1 3
1 2
4 5
```
**输出:**
```
2
3
```
**注意:**
在第一个测试用例中,第一次读取后,树将如下所示:

第二次读取后:

因此,Copil Copac需要2次读取来绘制这棵树。**题目大意:** 给定一棵树的n-1条边,这棵树有n个顶点。Copil Copac按照以下算法绘制这棵树: - 步骤0:绘制第一个顶点(顶点1),然后转到步骤1。 - 步骤1:按输入顺序检查每条边。如果边连接已经绘制过的顶点u和未绘制的顶点v,Copil Copac将绘制未绘制的顶点v和这条边。检查完每条边后,转到步骤2。 - 步骤2:如果所有顶点都已绘制,则终止算法。否则,转到步骤1。 读取次数定义为Copil Copac执行步骤1的次数。 求Copil Copac绘制整棵树需要的读取次数。 **输入数据格式:** 每个测试包含多个测试用例。第一行输入包含一个整数t(1≤t≤10^4)——测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数n(2≤n≤2×10^5)——树的顶点数量。 接下来每个测试用例包含n-1行,每行包含两个整数u_i和v_i(1≤u_i,v_i≤n,u_i≠v_i),表示(u_i,v_i)是列表中的第i条边。保证给定的边构成一棵树。 保证所有测试用例的n之和不超过2×10^5。 **输出数据格式:** 对于每个测试用例,输出Copil Copac绘制树需要的读取次数。 **示例:** **输入:** ``` 2 6 4 5 1 3 1 2 3 4 1 6 7 5 6 2 4 2 7 1 3 1 2 4 5 ``` **输出:** ``` 2 3 ``` **注意:** 在第一个测试用例中,第一次读取后,树将如下所示:  第二次读取后:  因此,Copil Copac需要2次读取来绘制这棵树。