310412: CF1829F. Forever Winter

A snowflake graph is generated from two integers $x$ and $y$, both greater than $1$, as follows:

• Start with one central vertex.
• Connect $x$ new vertices to this central vertex.
• Connect $y$ new vertices to each of these $x$ vertices.

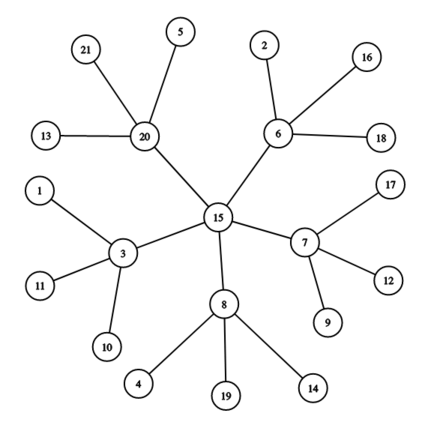
The snowflake graph above has a central vertex $15$, then $x=5$ vertices attached to it ($3$, $6$, $7$, $8$, and $20$), and then $y=3$ vertices attached to each of those.

The first line contains a single integer $t$ ($1 \leq t \leq 1000$) — the number of test cases.

The first line of each test case contains two integers $n$ and $m$ ($2 \leq n \leq 200$; $1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right)$) — the number of vertices and edges in the graph, respectively.

The next $m$ lines each contain two integers each $u$ and $v$ ($1 \leq u, v \leq n$, $u \neq v$) — the numbers of vertices connected by an edge. The graph does not contain multiple edges and self-loops.

It is guaranteed that this graph is a snowflake graph for some integers $x$ and $y$ both greater than $1$.

For each test case, on a separate line output the values of $x$ and $y$, in that order, separated by a space.

3
21 20
21 20
5 20
13 20
1 3
11 3
10 3
4 8
19 8
14 8
9 7
12 7
17 7
18 6
16 6
2 6
6 15
7 15
8 15
20 15
3 15
7 6
1 2
1 3
2 4
2 5
3 6
3 7
9 8
9 3
3 6
6 2
2 1
5 2
2 7
4 3
3 8

5 3
2 2
2 3

The first test case is pictured in the statement. Note that the output 3 5 is incorrect, since $x$ should be output before $y$.

题意翻译