310346: CF1817D. Toy Machine

D. Toy Machinetime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

There is a toy machine with toys arranged in two rows of $n$ cells each ($n$ is odd).

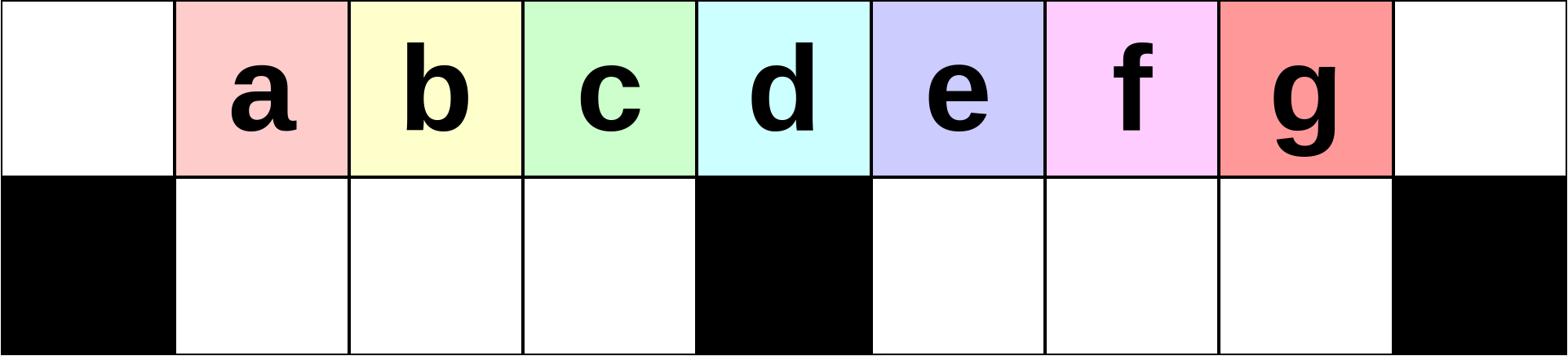Initial state for $n=9$.

Initially, $n-2$ toys are placed in the non-corner cells of the top row. The bottom row is initially empty, and its leftmost, rightmost, and central cells are blocked. There are $4$ buttons to control the toy machine: left, right, up, and down marked by the letters L, R, U, and D correspondingly.

When pressing L, R, U, or D, all the toys will be moved simultaneously in the corresponding direction and will only stop if they push into another toy, the wall or a blocked cell. Your goal is to move the $k$-th toy into the leftmost cell of the top row. The toys are numbered from $1$ to $n-2$ from left to right. Given $n$ and $k$, find a solution that uses at most $1\,000\,000$ button presses.

To test out the toy machine, a web page is available that lets you play the game in real time.

Input

The first and only line contains two integers, $n$ and $k$ ($5 \le n \le 100\,000$, $n$ is odd, $1 \le k \le n-2$) — the number of cells in a row, and the index of the toy that has to be moved to the leftmost cell of the top row.

Output

On a single line, output a description of the button presses as a string of at most $1\,000\,000$ characters. The string should only contain the characters L, R, U, and D. The $i$-th character in the string is the $i$-th button that is pressed. After all the button presses are performed, the $k$-th toy should be in the leftmost cell of the top row.

If there are multiple solutions, print any. The number of button presses does not have to be minimized.

ExamplesInput

5 1

Output

RDL

Input

7 2

Output

RDL

Note

In the first example, there will be $5-2 = 3$ toys. The first toy needs to end up in the leftmost cell of the top row. The moves RDL will achieve this, see the picture for a better understanding. Another possible solution would be to do one button press L.

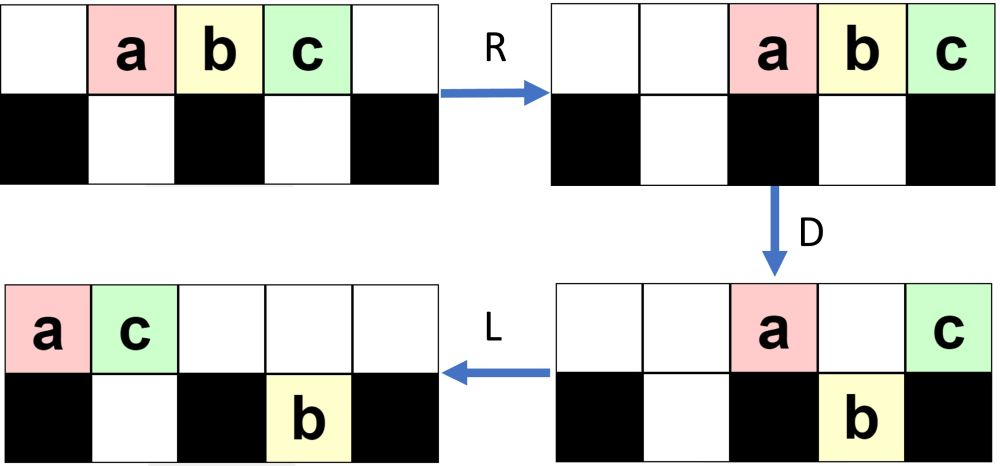Visualization of the moves for the first example.

题目大意：
有一个玩具机器，玩具分布在两行，每行有n个单元格（n是奇数）。最初，顶行除了角落的单元格外，其他单元格都放有一个玩具；底行最初是空的，其最左、最右和中间的单元格被阻塞。有4个按钮控制玩具机器：左、右、上、下，分别用字母L、R、U、D表示。当按L、R、U或D时，所有玩具将同时向相应方向移动，并且只有在推动另一个玩具、墙壁或被阻塞的单元格时才会停止。目标是将第k个玩具移动到顶行的最左边的单元格。玩具从左到右编号为1到n-2。给定n和k，找到使用最多1,000,000次按钮按压的解决方案。

输入数据格式：
第一行包含两个整数n和k（5≤n≤100,000，n是奇数，1≤k≤n-2）——一行中的单元格数和要移动到顶行最左边单元格的玩具的索引。

输出数据格式：
在一行中，输出一个最多有1,000,000个字符的字符串，描述按钮按压。字符串只能包含字符L、R、U和D。字符串中的第i个字符表示按下的第i个按钮。完成所有按钮按压后，第k个玩具应位于顶行的最左边的单元格。

如果存在多个解决方案，则可以输出任何一个。按钮按压次数不必最小化。

例：

输入
```
5 1
```
输出
```
RDL
```

输入
```
7 2
```
输出
```
RDL
```

注意：在第一个示例中，将有5-2=3个玩具。第一个玩具需要结束在顶行的最左边的单元格。RDL的移动将实现这一点。另一个可能的解决方案是做一个按钮按压L。题目大意： 有一个玩具机器，玩具分布在两行，每行有n个单元格（n是奇数）。最初，顶行除了角落的单元格外，其他单元格都放有一个玩具；底行最初是空的，其最左、最右和中间的单元格被阻塞。有4个按钮控制玩具机器：左、右、上、下，分别用字母L、R、U、D表示。当按L、R、U或D时，所有玩具将同时向相应方向移动，并且只有在推动另一个玩具、墙壁或被阻塞的单元格时才会停止。目标是将第k个玩具移动到顶行的最左边的单元格。玩具从左到右编号为1到n-2。给定n和k，找到使用最多1,000,000次按钮按压的解决方案。 输入数据格式： 第一行包含两个整数n和k（5≤n≤100,000，n是奇数，1≤k≤n-2）——一行中的单元格数和要移动到顶行最左边单元格的玩具的索引。 输出数据格式： 在一行中，输出一个最多有1,000,000个字符的字符串，描述按钮按压。字符串只能包含字符L、R、U和D。字符串中的第i个字符表示按下的第i个按钮。完成所有按钮按压后，第k个玩具应位于顶行的最左边的单元格。 如果存在多个解决方案，则可以输出任何一个。按钮按压次数不必最小化。 例： 输入 ``` 5 1 ``` 输出 ``` RDL ``` 输入 ``` 7 2 ``` 输出 ``` RDL ``` 注意：在第一个示例中，将有5-2=3个玩具。第一个玩具需要结束在顶行的最左边的单元格。RDL的移动将实现这一点。另一个可能的解决方案是做一个按钮按压L。