310249: CF1804H. Code Lock
Description
Lara has a safe that is locked with a circle-shaped code lock that consists of a rotating arrow, a static circumference around the arrow, an input screen, and an input button.
The circumference of the lock is split into $k$ equal sections numbered from $1$ to $k$ in clockwise order. Arrow always points to one of the sections. Each section is marked with one of the first $k$ letters of the English alphabet. No two sections are marked with the same letter.
Due to the lock limitations, the safe's password is a string of length $n$ that consists of first $k$ letters of the English alphabet only. Lara enters the password by rotating the lock's arrow and pressing the input button. Initially, the lock's arrow points to section $1$ and the input screen is empty. In one second she can do one of the following actions.
- Rotate the arrow one section clockwise. If the arrow was pointing at section $x < k$ it will now point at section $x + 1$. If the arrow was pointing at section $k$ it will now point at section $1$.
- Rotate the arrow one section counter-clockwise. If the arrow was pointing at section $x > 1$ it will now point at section $x - 1$. If the arrow was pointing at section $1$ it will now point at section $k$.
- Press the input button. The letter marked on the section that the arrow points to will be added to the content of the input screen.
Lara has recently found out that the safe can be re-programmed. She can take the first $k$ letters of the English alphabet and assign them to the sectors in any order she likes. Now she wants to re-arrange the letters in a way that will minimize the number of seconds it takes her to input the password. Compute this minimum number of seconds and the number of ways to assign letters, for which this minimum number of seconds is achieved.
Two ways to assign letters to sectors are considered to be distinct if there exists at least one sector $i$ that is assigned different letters.
InputThe first line of the input contains two integers $k$ and $n$ ($2 \leq k \leq 16$, $2 \leq n \leq 100\,000$) — the number of sectors on the lock's circumference and the length of Lara's password, respectively.
The second line of the input contains a string of length $n$ that consists of the first $k$ lowercase letters of the English alphabet only. This string is the password.
OutputOn the first line print minimum possible number of seconds it can take Lara to enter the password and open the safe if she assigns letters to sectors optimally.
On the second line print the number of ways to assign letters optimally.
ExamplesInput3 10 abcabcabcaOutput
19 2Input
4 20 bcbcbcbcadadadadcbdaOutput
40 2Input
4 6 adcbdaOutput
12 4Note
The initial states of optimal arrangements for the first example are shown in the figure below.
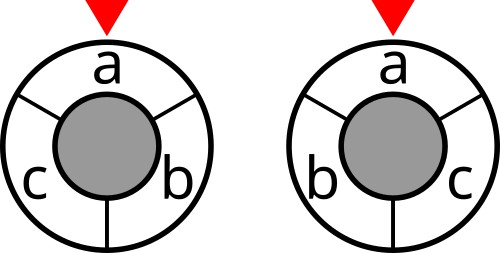
The initial states of optimal arrangements for the second example are shown in the figure below.
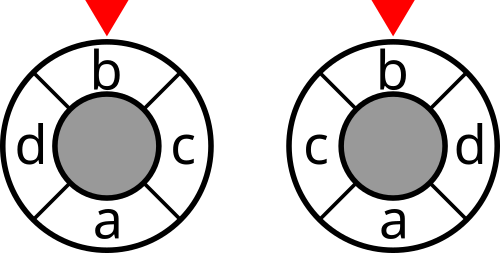
The initial states of optimal arrangements for the third example are shown in the figure below.
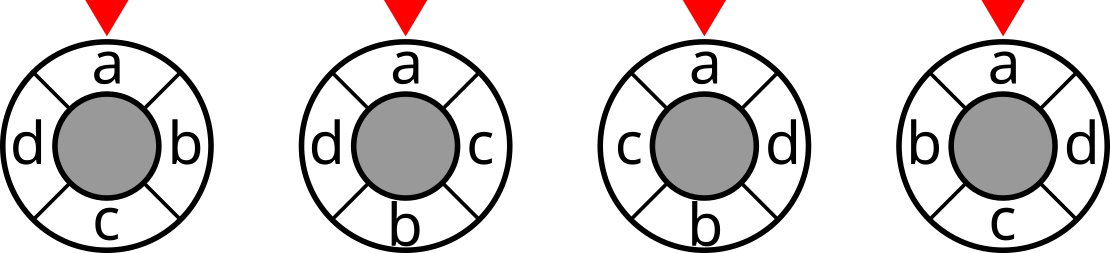
Input
Output
Lara有一个圆形的密码锁,锁由一个旋转箭头、围绕箭头的静态圆周、一个输入屏幕和一个输入按钮组成。锁的圆周被分成k个相等的部分,从1到k按顺时针方向编号。箭头总是指向其中一个部分。每个部分都标有英文字母表的前k个字母中的一个,没有两个部分标有相同的字母。
由于锁的限制,保险箱的密码是由长度为n的字符串组成,仅由英文字母表的前k个字母组成。Lara通过旋转锁的箭头并按下输入按钮来输入密码。最初,锁的箭头指向部分1,输入屏幕为空。在一秒钟内,她可以执行以下操作之一:
1. 顺时针旋转箭头一个部分。如果箭头指向部分x
3. 按下输入按钮。箭头指向的部分上标有的字母将被添加到输入屏幕的内容中。
输入屏幕的内容与密码匹配后,保险箱将打开。Lara总是以最短的时间输入密码。
Lara最近发现保险箱可以被重新编程。她可以取英文字母表的前k个字母,并以她喜欢的任何顺序分配给部分。现在她想要重新排列字母,以最小化输入密码所需的时间。计算这个最短时间以及实现这个最短时间的字母分配方式的数量。
输入输出数据格式:
输入:
第一行包含两个整数k和n(2≤k≤16,2≤n≤100,000)——锁圆周上的部分数和Lara密码的长度。
第二行包含一个长度为n的字符串,由英文字母表的前k个小写字母组成。这个字符串是密码。
输出:
第一行打印Lara在最优分配字母的情况下,输入密码并打开保险箱可能需要的最短秒数。
第二行打印最优分配字母的方式的数量。
示例:
输入:
3 10
abcabcabca
输出:
19
2
输入:
4 20
bcbcbcbcadadadadcbda
输出:
40
2
输入:
4 6
adcbda
输出:
12
4题目大意: Lara有一个圆形的密码锁,锁由一个旋转箭头、围绕箭头的静态圆周、一个输入屏幕和一个输入按钮组成。锁的圆周被分成k个相等的部分,从1到k按顺时针方向编号。箭头总是指向其中一个部分。每个部分都标有英文字母表的前k个字母中的一个,没有两个部分标有相同的字母。 由于锁的限制,保险箱的密码是由长度为n的字符串组成,仅由英文字母表的前k个字母组成。Lara通过旋转锁的箭头并按下输入按钮来输入密码。最初,锁的箭头指向部分1,输入屏幕为空。在一秒钟内,她可以执行以下操作之一: 1. 顺时针旋转箭头一个部分。如果箭头指向部分x