310188: CF1795D. Triangle Coloring
Memory Limit:512 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Triangle Coloring
题意翻译
### 简述题意 一共有 $n$ 条边( $n$ 是 $6$ 的倍数) ,每连续三条边构成一个三角形(比如若 $n=6$ 那么第 $1,2,3$ 条边构成一个三角形, $4,5,6$ 条边构成另一个三角形 ),每条边有一个权值 $w_i$ ,现在你可以把所有三角形的顶点涂成蓝色或红色,__且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点__,定义总权值为所有两端点颜色不同的边的权值和,问有多少种涂色方案可以使总权值最大(答案模 $998244353$ )。 ### 输入输出 输入共两行: 第一行一个整数 $n$ ,代表总边数。 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$ ,代表每条边的权值。 输出一个整数,代表总方案数模 $998244353$ 的值题目描述
You are given an undirected graph consisting of $ n $ vertices and $ n $ edges, where $ n $ is divisible by $ 6 $ . Each edge has a weight, which is a positive (greater than zero) integer. The graph has the following structure: it is split into $ \frac{n}{3} $ triples of vertices, the first triple consisting of vertices $ 1, 2, 3 $ , the second triple consisting of vertices $ 4, 5, 6 $ , and so on. Every pair of vertices from the same triple is connected by an edge. There are no edges between vertices from different triples. You have to paint the vertices of this graph into two colors, red and blue. Each vertex should have exactly one color, there should be exactly $ \frac{n}{2} $ red vertices and $ \frac{n}{2} $ blue vertices. The coloring is called valid if it meets these constraints. The weight of the coloring is the sum of weights of edges connecting two vertices with different colors. Let $ W $ be the maximum possible weight of a valid coloring. Calculate the number of valid colorings with weight $ W $ , and print it modulo $ 998244353 $ .输入输出格式
输入格式
The first line contains one integer $ n $ ( $ 6 \le n \le 3 \cdot 10^5 $ , $ n $ is divisible by $ 6 $ ). The second line contains $ n $ integers $ w_1, w_2, \dots, w_n $ ( $ 1 \le w_i \le 1000 $ ) — the weights of the edges. Edge $ 1 $ connects vertices $ 1 $ and $ 2 $ , edge $ 2 $ connects vertices $ 1 $ and $ 3 $ , edge $ 3 $ connects vertices $ 2 $ and $ 3 $ , edge $ 4 $ connects vertices $ 4 $ and $ 5 $ , edge $ 5 $ connects vertices $ 4 $ and $ 6 $ , edge $ 6 $ connects vertices $ 5 $ and $ 6 $ , and so on.
输出格式
Print one integer — the number of valid colorings with maximum possible weight, taken modulo $ 998244353 $ .
输入输出样例
输入样例 #1
12
1 3 3 7 8 5 2 2 2 2 4 2输出样例 #1
36输入样例 #2
6
4 2 6 6 6 4输出样例 #2
2说明
The following picture describes the graph from the first example test. 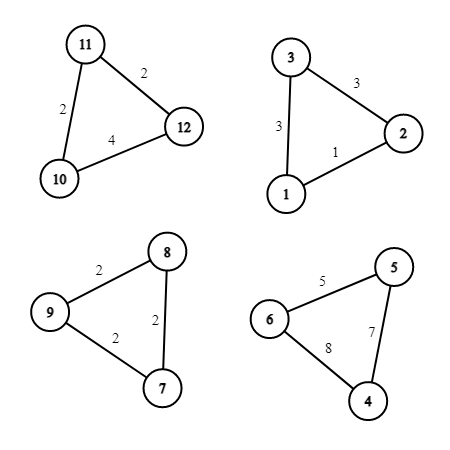The maximum possible weight of a valid coloring of this graph is $ 31 $ .Input
题意翻译
### 简述题意 一共有 $n$ 条边( $n$ 是 $6$ 的倍数) ,每连续三条边构成一个三角形(比如若 $n=6$ 那么第 $1,2,3$ 条边构成一个三角形, $4,5,6$ 条边构成另一个三角形 ),每条边有一个权值 $w_i$ ,现在你可以把所有三角形的顶点涂成蓝色或红色,__且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点__,定义总权值为所有两端点颜色不同的边的权值和,问有多少种涂色方案可以使总权值最大(答案模 $998244353$ )。 ### 输入输出 输入共两行: 第一行一个整数 $n$ ,代表总边数。 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$ ,代表每条边的权值。 输出一个整数,代表总方案数模 $998244353$ 的值Output
**题意翻译**
简述题意:
- 总共有 $n$ 条边($n$ 是 $6$ 的倍数),每连续三条边构成一个三角形(例如若 $n=6$,那么第 $1,2,3$ 条边构成一个三角形,$4,5,6$ 条边构成另一个三角形),每条边有一个权值 $w_i$。
- 现在可以把所有三角形的顶点涂成蓝色或红色,且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点。
- 定义总权值为所有两端点颜色不同的边的权值和。
- 问有多少种涂色方案可以使总权值最大(答案模 $998244353$)。
输入输出:
- 输入共两行:
- 第一行一个整数 $n$,代表总边数。
- 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$,代表每条边的权值。
- 输出一个整数,代表总方案数模 $998244353$ 的值。
**题目描述**
给定一个由 $n$ 个顶点和 $n$ 条边组成的无向图,其中 $n$ 是 $6$ 的倍数。每条边都有一个正整数(大于零)的权重。
图的构造如下:它被分成 $\frac{n}{3}$ 组顶点,第一组由顶点 $1, 2, 3$ 组成,第二组由顶点 $4, 5, 6$ 组成,依此类推。每一组内的顶点都通过边相连。不同组之间的顶点没有边相连。
你必须将图的顶点涂成两种颜色,红色和蓝色。每个顶点应该有且只有一种颜色,并且应该有 $\frac{n}{2}$ 个红色顶点和 $\frac{n}{2}$ 个蓝色顶点。如果一种涂色满足这些约束,则称为有效涂色。
涂色的权重是连接不同颜色顶点的边的权重之和。
设 $W$ 为有效涂色的最大可能权重。计算权重为 $W$ 的有效涂色数量,并模 $998244353$ 后输出。
**输入输出格式**
输入格式:
- 第一行包含一个整数 $n$($6 \le n \le 3 \times 10^5$,$n$ 是 $6$ 的倍数)。
- 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$($1 \le w_i \le 1000$)——边的权重。边 $1$ 连接顶点 $1$ 和 $2$,边 $2$ 连接顶点 $1$ 和 $3$,边 $3$ 连接顶点 $2$ 和 $3$,依此类推。
输出格式:
- 打印一个整数——权重最大的有效涂色数量,模 $998244353$ 后的值。
**输入输出样例**
输入样例 #1:
```
12
1 3 3 7 8 5 2 2 2 2 4 2
```
输出样例 #1:
```
36
```
输入样例 #2:
```
6
4 2 6 6 6 4
```
输出样例 #2:
```
2
```
**说明**
以下图片描述了第一个示例测试的图形。

这个图形的有效涂色的最大可能权重是 $31$。**题意翻译** 简述题意: - 总共有 $n$ 条边($n$ 是 $6$ 的倍数),每连续三条边构成一个三角形(例如若 $n=6$,那么第 $1,2,3$ 条边构成一个三角形,$4,5,6$ 条边构成另一个三角形),每条边有一个权值 $w_i$。 - 现在可以把所有三角形的顶点涂成蓝色或红色,且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点。 - 定义总权值为所有两端点颜色不同的边的权值和。 - 问有多少种涂色方案可以使总权值最大(答案模 $998244353$)。 输入输出: - 输入共两行: - 第一行一个整数 $n$,代表总边数。 - 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$,代表每条边的权值。 - 输出一个整数,代表总方案数模 $998244353$ 的值。 **题目描述** 给定一个由 $n$ 个顶点和 $n$ 条边组成的无向图,其中 $n$ 是 $6$ 的倍数。每条边都有一个正整数(大于零)的权重。 图的构造如下:它被分成 $\frac{n}{3}$ 组顶点,第一组由顶点 $1, 2, 3$ 组成,第二组由顶点 $4, 5, 6$ 组成,依此类推。每一组内的顶点都通过边相连。不同组之间的顶点没有边相连。 你必须将图的顶点涂成两种颜色,红色和蓝色。每个顶点应该有且只有一种颜色,并且应该有 $\frac{n}{2}$ 个红色顶点和 $\frac{n}{2}$ 个蓝色顶点。如果一种涂色满足这些约束,则称为有效涂色。 涂色的权重是连接不同颜色顶点的边的权重之和。 设 $W$ 为有效涂色的最大可能权重。计算权重为 $W$ 的有效涂色数量,并模 $998244353$ 后输出。 **输入输出格式** 输入格式: - 第一行包含一个整数 $n$($6 \le n \le 3 \times 10^5$,$n$ 是 $6$ 的倍数)。 - 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$($1 \le w_i \le 1000$)——边的权重。边 $1$ 连接顶点 $1$ 和 $2$,边 $2$ 连接顶点 $1$ 和 $3$,边 $3$ 连接顶点 $2$ 和 $3$,依此类推。 输出格式: - 打印一个整数——权重最大的有效涂色数量,模 $998244353$ 后的值。 **输入输出样例** 输入样例 #1: ``` 12 1 3 3 7 8 5 2 2 2 2 4 2 ``` 输出样例 #1: ``` 36 ``` 输入样例 #2: ``` 6 4 2 6 6 6 4 ``` 输出样例 #2: ``` 2 ``` **说明** 以下图片描述了第一个示例测试的图形。  这个图形的有效涂色的最大可能权重是 $31$。
简述题意:
- 总共有 $n$ 条边($n$ 是 $6$ 的倍数),每连续三条边构成一个三角形(例如若 $n=6$,那么第 $1,2,3$ 条边构成一个三角形,$4,5,6$ 条边构成另一个三角形),每条边有一个权值 $w_i$。
- 现在可以把所有三角形的顶点涂成蓝色或红色,且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点。
- 定义总权值为所有两端点颜色不同的边的权值和。
- 问有多少种涂色方案可以使总权值最大(答案模 $998244353$)。
输入输出:
- 输入共两行:
- 第一行一个整数 $n$,代表总边数。
- 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$,代表每条边的权值。
- 输出一个整数,代表总方案数模 $998244353$ 的值。
**题目描述**
给定一个由 $n$ 个顶点和 $n$ 条边组成的无向图,其中 $n$ 是 $6$ 的倍数。每条边都有一个正整数(大于零)的权重。
图的构造如下:它被分成 $\frac{n}{3}$ 组顶点,第一组由顶点 $1, 2, 3$ 组成,第二组由顶点 $4, 5, 6$ 组成,依此类推。每一组内的顶点都通过边相连。不同组之间的顶点没有边相连。
你必须将图的顶点涂成两种颜色,红色和蓝色。每个顶点应该有且只有一种颜色,并且应该有 $\frac{n}{2}$ 个红色顶点和 $\frac{n}{2}$ 个蓝色顶点。如果一种涂色满足这些约束,则称为有效涂色。
涂色的权重是连接不同颜色顶点的边的权重之和。
设 $W$ 为有效涂色的最大可能权重。计算权重为 $W$ 的有效涂色数量,并模 $998244353$ 后输出。
**输入输出格式**
输入格式:
- 第一行包含一个整数 $n$($6 \le n \le 3 \times 10^5$,$n$ 是 $6$ 的倍数)。
- 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$($1 \le w_i \le 1000$)——边的权重。边 $1$ 连接顶点 $1$ 和 $2$,边 $2$ 连接顶点 $1$ 和 $3$,边 $3$ 连接顶点 $2$ 和 $3$,依此类推。
输出格式:
- 打印一个整数——权重最大的有效涂色数量,模 $998244353$ 后的值。
**输入输出样例**
输入样例 #1:
```
12
1 3 3 7 8 5 2 2 2 2 4 2
```
输出样例 #1:
```
36
```
输入样例 #2:
```
6
4 2 6 6 6 4
```
输出样例 #2:
```
2
```
**说明**
以下图片描述了第一个示例测试的图形。

这个图形的有效涂色的最大可能权重是 $31$。**题意翻译** 简述题意: - 总共有 $n$ 条边($n$ 是 $6$ 的倍数),每连续三条边构成一个三角形(例如若 $n=6$,那么第 $1,2,3$ 条边构成一个三角形,$4,5,6$ 条边构成另一个三角形),每条边有一个权值 $w_i$。 - 现在可以把所有三角形的顶点涂成蓝色或红色,且要求有 $\frac{n}{2}$ 个蓝点和 $\frac{n}{2}$ 个红点。 - 定义总权值为所有两端点颜色不同的边的权值和。 - 问有多少种涂色方案可以使总权值最大(答案模 $998244353$)。 输入输出: - 输入共两行: - 第一行一个整数 $n$,代表总边数。 - 第二行共 $n$ 个整数,其中第 $i$ 个数为 $w_i$,代表每条边的权值。 - 输出一个整数,代表总方案数模 $998244353$ 的值。 **题目描述** 给定一个由 $n$ 个顶点和 $n$ 条边组成的无向图,其中 $n$ 是 $6$ 的倍数。每条边都有一个正整数(大于零)的权重。 图的构造如下:它被分成 $\frac{n}{3}$ 组顶点,第一组由顶点 $1, 2, 3$ 组成,第二组由顶点 $4, 5, 6$ 组成,依此类推。每一组内的顶点都通过边相连。不同组之间的顶点没有边相连。 你必须将图的顶点涂成两种颜色,红色和蓝色。每个顶点应该有且只有一种颜色,并且应该有 $\frac{n}{2}$ 个红色顶点和 $\frac{n}{2}$ 个蓝色顶点。如果一种涂色满足这些约束,则称为有效涂色。 涂色的权重是连接不同颜色顶点的边的权重之和。 设 $W$ 为有效涂色的最大可能权重。计算权重为 $W$ 的有效涂色数量,并模 $998244353$ 后输出。 **输入输出格式** 输入格式: - 第一行包含一个整数 $n$($6 \le n \le 3 \times 10^5$,$n$ 是 $6$ 的倍数)。 - 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$($1 \le w_i \le 1000$)——边的权重。边 $1$ 连接顶点 $1$ 和 $2$,边 $2$ 连接顶点 $1$ 和 $3$,边 $3$ 连接顶点 $2$ 和 $3$,依此类推。 输出格式: - 打印一个整数——权重最大的有效涂色数量,模 $998244353$ 后的值。 **输入输出样例** 输入样例 #1: ``` 12 1 3 3 7 8 5 2 2 2 2 4 2 ``` 输出样例 #1: ``` 36 ``` 输入样例 #2: ``` 6 4 2 6 6 6 4 ``` 输出样例 #2: ``` 2 ``` **说明** 以下图片描述了第一个示例测试的图形。  这个图形的有效涂色的最大可能权重是 $31$。