Timofey and Black-White Tree

题意翻译

ZYH 有一棵 $n$ 个节点的树，最初 $c_0$ 号节点是黑色，其余均为白色。 给定操作序列 $c_1,c_2,\cdots,c_{n-1}$，第 $i$ 次操作表示将 $c_i$ 号节点染黑。每次操作后，输出距离最近的两个黑点间的距离。两点 $u,v$ 间的距离定义为 $u\to v$ 的路径上经过的边的条数。 多组数据，$1\leq T \leq 10^4,2\leq n \leq 2\times 10^5,\sum n\leq 2\times 10^5$，节点编号均在 $[1,n]$ 内。 translated by @[StayAlone](https://www.luogu.com.cn/user/409236)

题目描述

Timofey came to a famous summer school and found a tree on $ n $ vertices. A tree is a connected undirected graph without cycles. Every vertex of this tree, except $ c_0 $ , is colored white. The vertex $ c_0 $ is colored black. Timofey wants to color all the vertices of this tree in black. To do this, he performs $ n - 1 $ operations. During the $ i $ -th operation, he selects the vertex $ c_i $ , which is currently white, and paints it black. Let's call the positivity of tree the minimum distance between all pairs of different black vertices in it. The distance between the vertices $ v $ and $ u $ is the number of edges on the path from $ v $ to $ u $ . After each operation, Timofey wants to know the positivity of the current tree.

输入输出格式

输入格式

The first line contains the integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of testcases. The first line of each testcase contains the integers $ n, c_0 $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 1 \le c_0 \le n $ ) — the number of vertices in the tree and index of the initial black vertex. The second line of each testcase contains $ n - 1 $ unique integers $ c_1, c_2, \dots, c_{n-1} $ ( $ 1 \le c_i \le n $ , $ c_i \ne c_0 $ ), where $ c_i $ is the vertex which is colored black during the $ i $ -th operation. Each of the next $ n - 1 $ row of each testcase contains the integers $ v_i, u_i $ ( $ 1 \le v_i, u_i \le n $ ) — edges in the tree. It is guaranteed that the sum of $ n $ for all testcases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each testcase, print $ n - 1 $ integer on a separate line. The integer with index $ i $ must be equal to positivity of the tree obtained by the first $ i $ operations.

输入输出样例

输入样例 #1

6
6 6
4 1 3 5 2
2 4
6 5
5 3
3 4
1 3
4 2
4 1 3
3 1
2 3
1 4
10 3
10 7 6 5 2 9 8 1 4
1 2
1 3
4 5
4 3
6 4
8 7
9 8
10 8
1 8
7 3
7 5 1 2 4 6
1 2
3 2
4 5
3 4
6 5
7 6
9 7
9 3 1 4 2 6 8 5
4 1
8 9
4 8
2 6
7 3
2 4
3 5
5 4
10 2
1 8 5 10 6 9 4 3 7
10 7
7 8
3 6
9 7
7 6
4 2
1 6
7 5
9 2

输出样例 #1

3 2 1 1 1 
3 1 1 
3 2 2 2 2 2 1 1 1 
4 2 2 1 1 1 
5 1 1 1 1 1 1 1 
4 3 2 2 1 1 1 1 1

说明

In the first testcase, after the second operation, the tree looks like this: 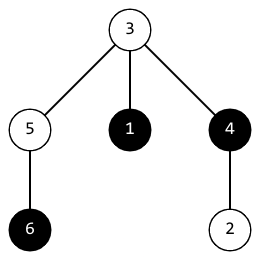 The distance between vertices $ 1 $ and $ 6 $ is $ 3 $ , the distance between vertices $ 4 $ and $ 6 $ is $ 3 $ , the distance between vertices $ 1 $ and $ 4 $ is $ 2 $ . The positivity of this tree is equal to the minimum of these distances. It equals $ 2 $ . In the third testcase, after the fourth operation, the tree looks like this: 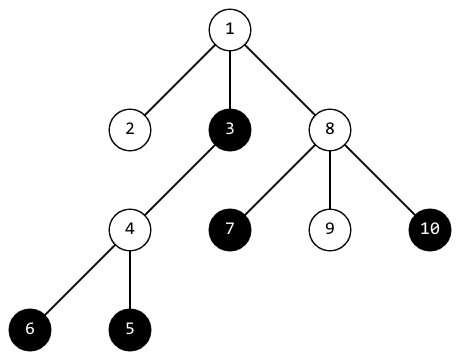 The positivity of this tree is $ 2 $ .

题目大意：

提莫非有一棵有n个节点的树，最初c_0号节点是黑色，其余都是白色。给定操作序列c_1,c_2,…,c_{n-1}，第i次操作表示将c_i号节点染黑。每次操作后，输出最近的两个黑点之间的距离。两点u,v之间的距离定义为u到v的路径上经过的边的条数。有多组数据，1≤T≤10^4,2≤n≤2×10^5,∑n≤2×10^5，节点编号都在[1,n]内。

输入输出数据格式：

输入格式：

第一行包含整数t(1≤t≤10^4)——测试用例的数量。

每个测试用例的第一行包含整数n,c_0(2≤n≤2×10^5,1≤c_0≤n)——树中的顶点数和初始黑色顶点的索引。

每个测试用例的第二行包含n-1个唯一的整数c_1,c_2,…,c_{n-1}(1≤c_i≤n,c_i≠c_0)，其中c_i是在第i次操作中染成黑色的顶点。

每个测试用例的接下来n-1行包含整数v_i,u_i(1≤v_i,u_i≤n)——树中的边。

保证所有测试用例的n之和不超过2×10^5。

输出格式：

对于每个测试用例，在一行中打印n-1个整数。

索引为i的整数必须等于通过前i次操作得到的树的积极性。题目大意： 提莫非有一棵有n个节点的树，最初c_0号节点是黑色，其余都是白色。给定操作序列c_1,c_2,…,c_{n-1}，第i次操作表示将c_i号节点染黑。每次操作后，输出最近的两个黑点之间的距离。两点u,v之间的距离定义为u到v的路径上经过的边的条数。有多组数据，1≤T≤10^4,2≤n≤2×10^5,∑n≤2×10^5，节点编号都在[1,n]内。 输入输出数据格式： 输入格式： 第一行包含整数t(1≤t≤10^4)——测试用例的数量。 每个测试用例的第一行包含整数n,c_0(2≤n≤2×10^5,1≤c_0≤n)——树中的顶点数和初始黑色顶点的索引。 每个测试用例的第二行包含n-1个唯一的整数c_1,c_2,…,c_{n-1}(1≤c_i≤n,c_i≠c_0)，其中c_i是在第i次操作中染成黑色的顶点。 每个测试用例的接下来n-1行包含整数v_i,u_i(1≤v_i,u_i≤n)——树中的边。 保证所有测试用例的n之和不超过2×10^5。 输出格式： 对于每个测试用例，在一行中打印n-1个整数。 索引为i的整数必须等于通过前i次操作得到的树的积极性。