Weighed Tree Radius

题意翻译

## 题目描述 给你一个$n$个点的树和$n-1$条边。第$i$个点的初始权值为$a_i$。 定义结点$v$到结点$u$的距离$d_v(u)$等于$v$和$u$之间的边的数量。注意:$d_v(u)=d_u(v),d_v(v)=0$ 定义结点$v$到结点$u$的权值距离$w_v(u)=d_v(u)+a_u$。注意：$w_v(u)=a_v,w_v(u) \neq w_u(v)$如果$a_u \neq a_v$ 与通常的距离类似，让我们定义结点$v$的偏心距$e(v)$是从$v$到其他结点的最大**权值距离（包括$v$本身）**，即$e(v)=\max\limits_{1\leq u \leq n} w_v(u)$。 最后，我们定义树的半径$r$是所有偏心距的最小值，即$r=\min\limits_{1\leq v\leq n} e(v)$ 你需要对$m$次询问进行回答，对于第$j$次询问，给出两个数$v_j$和$x_j$，表示将$a_{v_j}$的值修改为$x_j$。 在每次询问后，输出当前该树的半径$r$。 ## 输入格式 第一行包含一个整数$n(2\leq n \leq2\cdot10^5)$，表示树的结点个数。 第二行包含$n$个整数$a_1,\dots,a_n(0\leq a_i\leq 10^6)$，表示每个节点的初始权值。 接下来$n-1$行表示树的边。第$i$行包含两个整数$u_i$和$v_i(1\leq u_i,v_i\leq n;u_i \neq v_i)$，表示树的一条边。 接下来一行包含一个整数$m$，表示查询的个数。 接下来$m$行每行包含一个询问。第$j$个询问包含两个整数$v_j$和$x_j(1\leq v_j\leq n;0\leq x_j\leq10^6)$，表示询问的结点和该结点的新权值。 ## 输出格式 输出$m$个整数，表示每个查询后树的半径$r$。 ## 说明/提示 第一个询问后，你会得到下面这样的树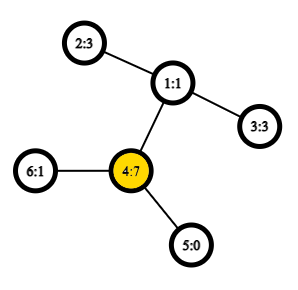：  图中被标记的结点是偏心距$e(v)$最小的结点，即$r=e(4)=7$。其他结点的偏心距如下:$e(1)=8,e(2)=9,e(3)=9,e(5)=8,e(6)=8$。 第二个询问后，你会得到下面这样的树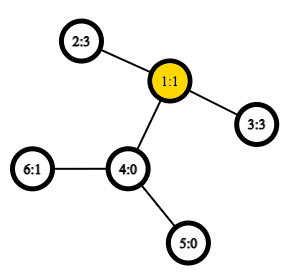：  半径$r=e(1)=4$ 第三个询问后，半径$r=e(2)=5$。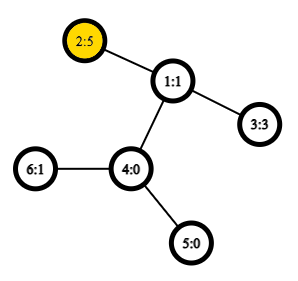 

题目描述

You are given a tree of $ n $ vertices and $ n - 1 $ edges. The $ i $ -th vertex has an initial weight $ a_i $ . Let the distance $ d_v(u) $ from vertex $ v $ to vertex $ u $ be the number of edges on the path from $ v $ to $ u $ . Note that $ d_v(u) = d_u(v) $ and $ d_v(v) = 0 $ . Let the weighted distance $ w_v(u) $ from $ v $ to $ u $ be $ w_v(u) = d_v(u) + a_u $ . Note that $ w_v(v) = a_v $ and $ w_v(u) \neq w_u(v) $ if $ a_u \neq a_v $ . Analogically to usual distance, let's define the eccentricity $ e(v) $ of vertex $ v $ as the greatest weighted distance from $ v $ to any other vertex (including $ v $ itself), or $ e(v) = \max\limits_{1 \le u \le n}{w_v(u)} $ . Finally, let's define the radius $ r $ of the tree as the minimum eccentricity of any vertex, or $ r = \min\limits_{1 \le v \le n}{e(v)} $ . You need to perform $ m $ queries of the following form: - $ v_j $ $ x_j $ — assign $ a_{v_j} = x_j $ . After performing each query, print the radius $ r $ of the current tree.

输入输出格式

输入格式

The first line contains the single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. The second line contains $ n $ integers $ a_1, \dots, a_n $ ( $ 0 \le a_i \le 10^6 $ ) — the initial weights of vertices. Next $ n - 1 $ lines contain edges of tree. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \neq v_i $ ) — the corresponding edge. The given edges form a tree. The next line contains the single integer $ m $ ( $ 1 \le m \le 10^5 $ ) — the number of queries. Next $ m $ lines contain queries — one query per line. The $ j $ -th query contains two integers $ v_j $ and $ x_j $ ( $ 1 \le v_j \le n $ ; $ 0 \le x_j \le 10^6 $ ) — a vertex and it's new weight.

输出格式

Print $ m $ integers — the radius $ r $ of the tree after performing each query.

输入输出样例

输入样例 #1

6
1 3 3 7 0 1
2 1
1 3
1 4
5 4
4 6
5
4 7
4 0
2 5
5 10
5 5

输出样例 #1

7
4
5
10
7

说明

After the first query, you have the following tree:  The marked vertex in the picture is the vertex with minimum $ e(v) $ , or $ r = e(4) = 7 $ . The eccentricities of the other vertices are the following: $ e(1) = 8 $ , $ e(2) = 9 $ , $ e(3) = 9 $ , $ e(5) = 8 $ , $ e(6) = 8 $ .The tree after the second query:  The radius $ r = e(1) = 4 $ .After the third query, the radius $ r = e(2) = 5 $ : 

**题目大意：**

给定一棵包含n个顶点和n-1条边的树，每个顶点都有一个初始权值。定义顶点v到顶点u的距离为它们之间边的数量，顶点v到顶点u的权值距离为距离加上顶点u的权值。顶点v的偏心距是它到其他顶点的最大权值距离，树的半径是所有顶点偏心距的最小值。每次查询会改变一个顶点的权值，要求输出每次查询后树的半径。

**输入数据格式：**

- 第一行：整数n（2≤n≤2×10^5），表示树的顶点数。
- 第二行：n个整数，表示每个顶点的初始权值（0≤权值≤10^6）。
- 接下来n-1行：每行两个整数，表示树的一条边。
- 接下来一行：整数m，表示查询次数。
- 接下来m行：每行两个整数，表示查询的顶点和该顶点的新权值。

**输出数据格式：**

- m个整数，表示每次查询后树的半径。

**输入输出样例：**

**输入样例 #1:**
```
6
1 3 3 7 0 1
2 1
1 3
1 4
5 4
4 6
5
4 7
4 0
2 5
5 10
5 5
```

**输出样例 #1:**
```
7
4
5
10
7
```

**说明：**

每次查询后，会更新树的权值并计算新的半径。半径是树中所有顶点偏心距的最小值，偏心距是一个顶点到其他顶点的最大权值距离。**题目大意：** 给定一棵包含n个顶点和n-1条边的树，每个顶点都有一个初始权值。定义顶点v到顶点u的距离为它们之间边的数量，顶点v到顶点u的权值距离为距离加上顶点u的权值。顶点v的偏心距是它到其他顶点的最大权值距离，树的半径是所有顶点偏心距的最小值。每次查询会改变一个顶点的权值，要求输出每次查询后树的半径。 **输入数据格式：** - 第一行：整数n（2≤n≤2×10^5），表示树的顶点数。 - 第二行：n个整数，表示每个顶点的初始权值（0≤权值≤10^6）。 - 接下来n-1行：每行两个整数，表示树的一条边。 - 接下来一行：整数m，表示查询次数。 - 接下来m行：每行两个整数，表示查询的顶点和该顶点的新权值。 **输出数据格式：** - m个整数，表示每次查询后树的半径。 **输入输出样例：** **输入样例 #1:** ``` 6 1 3 3 7 0 1 2 1 1 3 1 4 5 4 4 6 5 4 7 4 0 2 5 5 10 5 5 ``` **输出样例 #1:** ``` 7 4 5 10 7 ``` **说明：** 每次查询后，会更新树的权值并计算新的半径。半径是树中所有顶点偏心距的最小值，偏心距是一个顶点到其他顶点的最大权值距离。