310079: CF1779G. The Game of the Century
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
The Game of the Century
题目描述
The time has finally come, MKnez and Baltic are to host The Game of the Century. For that purpose, they built a village to lodge its participants. The village has the shape of an equilateral triangle delimited by three roads of length $ n $ . It is cut into $ n^2 $ smaller equilateral triangles, of side length $ 1 $ , by $ 3n-3 $ additional roads which run parallel to the sides. See the figure for $ n=3 $ . Each of the $ 3n $ roads is made of multiple (possibly $ 1 $ ) road segments of length $ 1 $ which connect adjacent intersections. 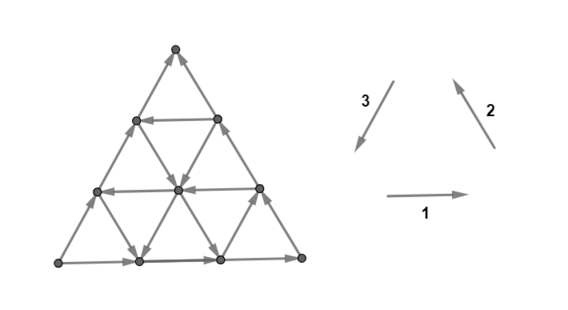The direction has already been chosen for each of the $ 3n $ roads (so, for each road, the same direction is assigned to all its road segments). Traffic can only go in the specified directions (i. e. the roads are monodirectional). You are tasked with making adjustments to the traffic plan so that from each intersection it is possible to reach every other intersection. Specifically, you can invert the traffic direction of any number of road segments of length $ 1 $ . What is the minimal number of road segments for which you need to invert the traffic direction?输入输出格式
输入格式
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10\,000 $ ). The description of the test cases follows. The first line of each test case contains a positive integer $ n $ ( $ 1\leq n\leq 10^5 $ ) — the size of the triangular village's sides. Three lines follow, each containing a binary string of length $ n $ which describes the traffic directions of the roads. The $ i $ -th of the following three lines contains a binary string $ s_i $ of length $ n $ representing the direction of each road parallel to the road segment denoted by $ i $ in the picture above. In particular, the $ j $ -th character of $ s_i $ is "1" if the $ j $ -th shortest road (parallel to the road segment denoted by $ i $ in the picture) has the same direction of the road segment denoted by $ i $ in the picture, while it is "0" if it has the opposite direction. So the first character of $ s_i $ describes the direction of the road containing only $ 1 $ road segment, while the last character describes the direction of the road containing $ n $ road segments. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .
输出格式
For each test case, print the minimum number of road segments for which you need to invert the traffic direction.
输入输出样例
输入样例 #1
3
3
001
001
010
1
0
0
0
3
111
011
100输出样例 #1
2
0
3说明
The first example corresponds to the picture in the statement. There exist multiple solutions that invert the traffic direction of exactly $ 2 $ road segments, but inverting only $ 1 $ road segment never makes it possible to reach every intersection from any other. One of the possible solutions is shown in the picture below in which the inverted road segments are highlighted in blue. 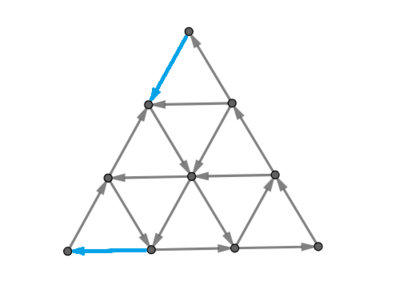In the second example, the answer is $ 0 $ since it is already possible to reach every intersection from any other.Input
暂时还没有翻译
Output
**世纪游戏**
**题目描述**
终于到了这个时刻,MKnez和Baltic即将举办世纪游戏。为此,他们建造了一个村庄来容纳参赛者。
村庄呈等边三角形,由三条长度为 $ n $ 的道路界定。通过 $ 3n-3 $ 条额外的与边平行的道路,它被切成 $ n^2 $ 个更小的边长为 $ 1 $ 的等边三角形。对于 $ n=3 $ 的情况,请参考下图。每条 $ 3n $ 道路由多个(可能为 $ 1 $ 个)长度为 $ 1 $ 的路段组成,这些路段连接相邻的交叉口。

每条 $ 3n $ 道路的方向已经确定(所以,对于每条道路,所有其路段都被分配了相同的方向)。交通只能按照指定的方向行驶(即道路是单向的)。
你的任务是调整交通计划,使得从每个交叉口都可以到达其他任何一个交叉口。具体来说,你可以反转任意数量的长度为 $ 1 $ 的路段的交通方向。你需要反转交通方向的最小路段数量是多少?
**输入输出格式**
**输入格式**
每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $ ( $ 1 \leq t \leq 10\,000 $ )。接下来是测试用例的描述。
每个测试用例的第一行包含一个正整数 $ n $ ( $ 1\leq n\leq 10^5 $ ) —— 三角形村庄边长的大小。
接下来三行,每行包含一个长度为 $ n $ 的二进制字符串,描述了道路的交通方向。
接下来的三行中的每一行包含一个二进制字符串 $ s_i $,长度为 $ n $,表示与图片中由 $ i $ 标记的道路段平行的每条道路的方向。特别是,如果 $ s_i $ 的第 $ j $ 个字符是 "1",则表示与图片中由 $ i $ 标记的道路段有相同方向的最短的第 $ j $ 条道路(与图片中由 $ i $ 标记的道路段平行),如果是 "0",则表示方向相反。所以 $ s_i $ 的第一个字符描述了只包含 $ 1 $ 个路段的道路的方向,而最后一个字符描述了包含 $ n $ 个路段的道路的方向。
保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。
**输出格式**
对于每个测试用例,打印你需要反转交通方向的最小路段数量。
**输入输出样例**
**输入样例 #1**
```
3
3
001
001
010
1
0
0
0
3
111
011
100
```
**输出样例 #1**
```
2
0
3
```
**说明**
第一个示例对应于题目描述中的图片。存在多种反转恰好 $ 2 $ 个路段交通方向的解决方案,但仅反转 $ 1 $ 个路段的解决方案永远不会使从一个交叉口到达任何其他交叉口成为可能。可能的解决方案之一在下面的图片中用蓝色突出显示的反转路段。

在第二个示例中,答案是 $ 0 $,因为已经可以从任一交叉口到达其他所有交叉口。**世纪游戏** **题目描述** 终于到了这个时刻,MKnez和Baltic即将举办世纪游戏。为此,他们建造了一个村庄来容纳参赛者。 村庄呈等边三角形,由三条长度为 $ n $ 的道路界定。通过 $ 3n-3 $ 条额外的与边平行的道路,它被切成 $ n^2 $ 个更小的边长为 $ 1 $ 的等边三角形。对于 $ n=3 $ 的情况,请参考下图。每条 $ 3n $ 道路由多个(可能为 $ 1 $ 个)长度为 $ 1 $ 的路段组成,这些路段连接相邻的交叉口。  每条 $ 3n $ 道路的方向已经确定(所以,对于每条道路,所有其路段都被分配了相同的方向)。交通只能按照指定的方向行驶(即道路是单向的)。 你的任务是调整交通计划,使得从每个交叉口都可以到达其他任何一个交叉口。具体来说,你可以反转任意数量的长度为 $ 1 $ 的路段的交通方向。你需要反转交通方向的最小路段数量是多少? **输入输出格式** **输入格式** 每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $ ( $ 1 \leq t \leq 10\,000 $ )。接下来是测试用例的描述。 每个测试用例的第一行包含一个正整数 $ n $ ( $ 1\leq n\leq 10^5 $ ) —— 三角形村庄边长的大小。 接下来三行,每行包含一个长度为 $ n $ 的二进制字符串,描述了道路的交通方向。 接下来的三行中的每一行包含一个二进制字符串 $ s_i $,长度为 $ n $,表示与图片中由 $ i $ 标记的道路段平行的每条道路的方向。特别是,如果 $ s_i $ 的第 $ j $ 个字符是 "1",则表示与图片中由 $ i $ 标记的道路段有相同方向的最短的第 $ j $ 条道路(与图片中由 $ i $ 标记的道路段平行),如果是 "0",则表示方向相反。所以 $ s_i $ 的第一个字符描述了只包含 $ 1 $ 个路段的道路的方向,而最后一个字符描述了包含 $ n $ 个路段的道路的方向。 保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。 **输出格式** 对于每个测试用例,打印你需要反转交通方向的最小路段数量。 **输入输出样例** **输入样例 #1** ``` 3 3 001 001 010 1 0 0 0 3 111 011 100 ``` **输出样例 #1** ``` 2 0 3 ``` **说明** 第一个示例对应于题目描述中的图片。存在多种反转恰好 $ 2 $ 个路段交通方向的解决方案,但仅反转 $ 1 $ 个路段的解决方案永远不会使从一个交叉口到达任何其他交叉口成为可能。可能的解决方案之一在下面的图片中用蓝色突出显示的反转路段。  在第二个示例中,答案是 $ 0 $,因为已经可以从任一交叉口到达其他所有交叉口。
**题目描述**
终于到了这个时刻,MKnez和Baltic即将举办世纪游戏。为此,他们建造了一个村庄来容纳参赛者。
村庄呈等边三角形,由三条长度为 $ n $ 的道路界定。通过 $ 3n-3 $ 条额外的与边平行的道路,它被切成 $ n^2 $ 个更小的边长为 $ 1 $ 的等边三角形。对于 $ n=3 $ 的情况,请参考下图。每条 $ 3n $ 道路由多个(可能为 $ 1 $ 个)长度为 $ 1 $ 的路段组成,这些路段连接相邻的交叉口。

每条 $ 3n $ 道路的方向已经确定(所以,对于每条道路,所有其路段都被分配了相同的方向)。交通只能按照指定的方向行驶(即道路是单向的)。
你的任务是调整交通计划,使得从每个交叉口都可以到达其他任何一个交叉口。具体来说,你可以反转任意数量的长度为 $ 1 $ 的路段的交通方向。你需要反转交通方向的最小路段数量是多少?
**输入输出格式**
**输入格式**
每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $ ( $ 1 \leq t \leq 10\,000 $ )。接下来是测试用例的描述。
每个测试用例的第一行包含一个正整数 $ n $ ( $ 1\leq n\leq 10^5 $ ) —— 三角形村庄边长的大小。
接下来三行,每行包含一个长度为 $ n $ 的二进制字符串,描述了道路的交通方向。
接下来的三行中的每一行包含一个二进制字符串 $ s_i $,长度为 $ n $,表示与图片中由 $ i $ 标记的道路段平行的每条道路的方向。特别是,如果 $ s_i $ 的第 $ j $ 个字符是 "1",则表示与图片中由 $ i $ 标记的道路段有相同方向的最短的第 $ j $ 条道路(与图片中由 $ i $ 标记的道路段平行),如果是 "0",则表示方向相反。所以 $ s_i $ 的第一个字符描述了只包含 $ 1 $ 个路段的道路的方向,而最后一个字符描述了包含 $ n $ 个路段的道路的方向。
保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。
**输出格式**
对于每个测试用例,打印你需要反转交通方向的最小路段数量。
**输入输出样例**
**输入样例 #1**
```
3
3
001
001
010
1
0
0
0
3
111
011
100
```
**输出样例 #1**
```
2
0
3
```
**说明**
第一个示例对应于题目描述中的图片。存在多种反转恰好 $ 2 $ 个路段交通方向的解决方案,但仅反转 $ 1 $ 个路段的解决方案永远不会使从一个交叉口到达任何其他交叉口成为可能。可能的解决方案之一在下面的图片中用蓝色突出显示的反转路段。

在第二个示例中,答案是 $ 0 $,因为已经可以从任一交叉口到达其他所有交叉口。**世纪游戏** **题目描述** 终于到了这个时刻,MKnez和Baltic即将举办世纪游戏。为此,他们建造了一个村庄来容纳参赛者。 村庄呈等边三角形,由三条长度为 $ n $ 的道路界定。通过 $ 3n-3 $ 条额外的与边平行的道路,它被切成 $ n^2 $ 个更小的边长为 $ 1 $ 的等边三角形。对于 $ n=3 $ 的情况,请参考下图。每条 $ 3n $ 道路由多个(可能为 $ 1 $ 个)长度为 $ 1 $ 的路段组成,这些路段连接相邻的交叉口。  每条 $ 3n $ 道路的方向已经确定(所以,对于每条道路,所有其路段都被分配了相同的方向)。交通只能按照指定的方向行驶(即道路是单向的)。 你的任务是调整交通计划,使得从每个交叉口都可以到达其他任何一个交叉口。具体来说,你可以反转任意数量的长度为 $ 1 $ 的路段的交通方向。你需要反转交通方向的最小路段数量是多少? **输入输出格式** **输入格式** 每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $ ( $ 1 \leq t \leq 10\,000 $ )。接下来是测试用例的描述。 每个测试用例的第一行包含一个正整数 $ n $ ( $ 1\leq n\leq 10^5 $ ) —— 三角形村庄边长的大小。 接下来三行,每行包含一个长度为 $ n $ 的二进制字符串,描述了道路的交通方向。 接下来的三行中的每一行包含一个二进制字符串 $ s_i $,长度为 $ n $,表示与图片中由 $ i $ 标记的道路段平行的每条道路的方向。特别是,如果 $ s_i $ 的第 $ j $ 个字符是 "1",则表示与图片中由 $ i $ 标记的道路段有相同方向的最短的第 $ j $ 条道路(与图片中由 $ i $ 标记的道路段平行),如果是 "0",则表示方向相反。所以 $ s_i $ 的第一个字符描述了只包含 $ 1 $ 个路段的道路的方向,而最后一个字符描述了包含 $ n $ 个路段的道路的方向。 保证所有测试用例的 $ n $ 之和不超过 $ 10^5 $。 **输出格式** 对于每个测试用例,打印你需要反转交通方向的最小路段数量。 **输入输出样例** **输入样例 #1** ``` 3 3 001 001 010 1 0 0 0 3 111 011 100 ``` **输出样例 #1** ``` 2 0 3 ``` **说明** 第一个示例对应于题目描述中的图片。存在多种反转恰好 $ 2 $ 个路段交通方向的解决方案,但仅反转 $ 1 $ 个路段的解决方案永远不会使从一个交叉口到达任何其他交叉口成为可能。可能的解决方案之一在下面的图片中用蓝色突出显示的反转路段。  在第二个示例中,答案是 $ 0 $,因为已经可以从任一交叉口到达其他所有交叉口。