Score of a Tree

题意翻译

给你一个 $n$ 个结点根为 $1$ 的树。在 $t = 0$ 时，每个结点都有一个值，为 $0$ 或 $1$。 在每一个 $t > 0$ 时，每个结点的值都会变成其子结点在 $t - 1$ 时的值的异或和。 定义 $S(t)$ 为 $t$ 时所有结点值的和。 定义 $F(A)$ 为树在 $0 \le t \le 10^{100}$ 中所有 $S(t)$ 的和。其中 $A$ 为树在时刻 $0$ 时每个结点的值。 求所有 $2^n$ 个 $F(A)$ 的和。

题目描述

You are given a tree of $ n $ nodes, rooted at $ 1 $ . Every node has a value of either $ 0 $ or $ 1 $ at time $ t=0 $ . At any integer time $ t>0 $ , the value of a node becomes the [bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) of the values of its children at time $ t - 1 $ ; the values of leaves become $ 0 $ since they don't have any children. Let $ S(t) $ denote the sum of values of all nodes at time $ t $ . Let $ F(A) $ denote the sum of $ S(t) $ across all values of $ t $ such that $ 0 \le t \le 10^{100} $ , where $ A $ is the initial assignment of $ 0 $ s and $ 1 $ s in the tree. The task is to find the sum of $ F(A) $ for all $ 2^n $ initial configurations of $ 0 $ s and $ 1 $ s in the tree. Print the sum modulo $ 10^9+7 $ .

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). The description of the test cases follows. The first line of each test case contains $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the number of nodes in the tree. The next $ n-1 $ lines of each test case contain two integers each — $ u $ , $ v $ indicating an edge between $ u $ and $ v $ ( $ 1 \le u, v \le n $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

Output the sum modulo $ 10^9+7 $ for each test case.

输入输出样例

输入样例 #1

1
6
1 2
1 3
3 4
3 5
3 6

输出样例 #1

288

说明

Let us find $ F(A) $ for the configuration $ A = [0,1,0,0,1,1] $ ( $ A[i] $ denotes the value of node $ i $ ). Initially (at $ t = 0 $ ) our tree is as shown in the picture below. In each node, two values are shown: the number and the value of this node. $ S(0) $ for this configuration is $ 3 $ . 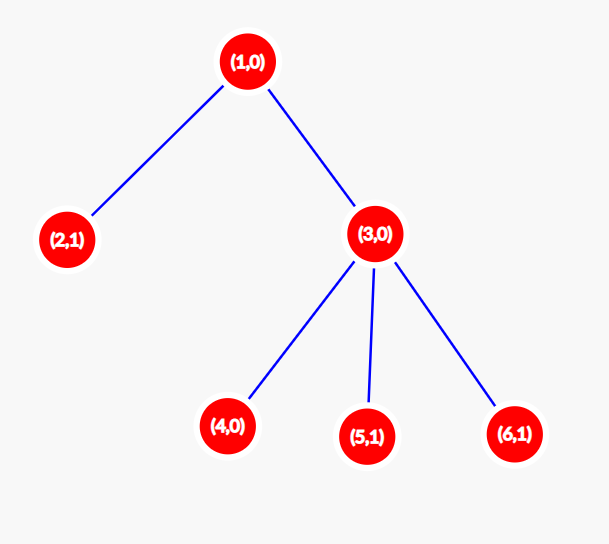At $ t = 1 $ the configuration changes to $ [1,0,0,0,0,0] $ . The tree looks as shown below. $ S(1) = 1 $ . 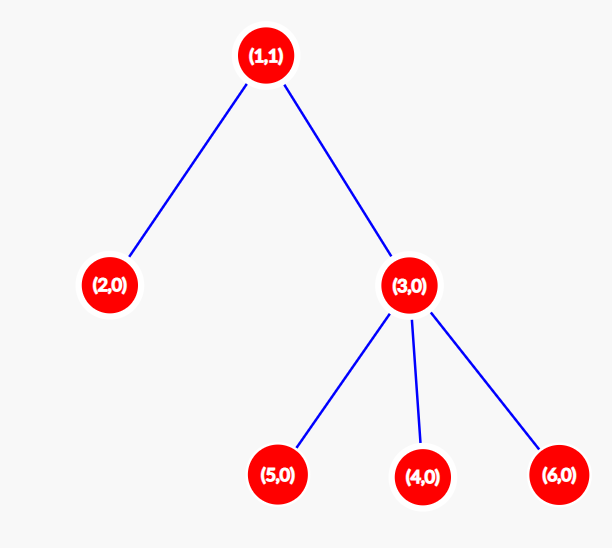At $ t = 2 $ the configuration changes to $ [0,0,0,0,0,0] $ . The tree looks as shown below. $ S(2) = 0 $ . 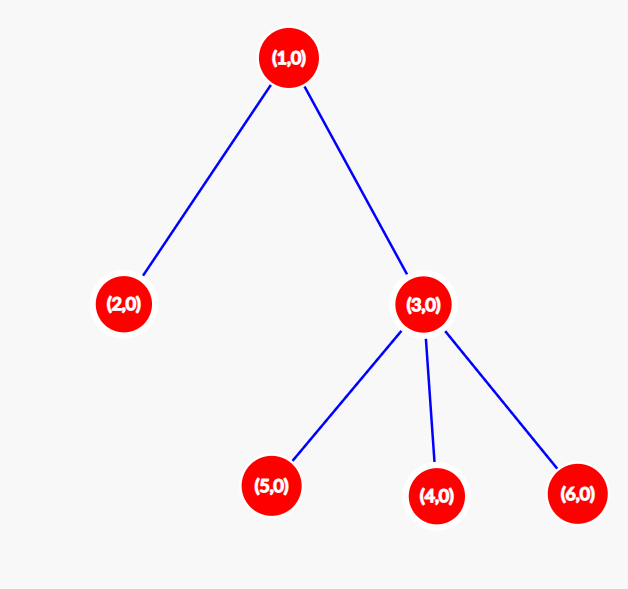For all $ t>2 $ , the graph remains unchanged, so $ S(t)=0 $ for all $ t > 2 $ . So, for the initial configuration $ A = [0,1,0,0,1,1] $ , the value of $ F(A) = 3 + 1 = 4 $ . Doing this process for all possible $ 2^{6} $ configurations yields us an answer of $ \textbf{288} $ .

题意翻译

给你一个 $n$ 个结点根为 $1$ 的树。在 $t = 0$ 时，每个结点都有一个值，为 $0$ 或 $1$。 在每一个 $t > 0$ 时，每个结点的值都会变成其子结点在 $t - 1$ 时的值的异或和。 定义 $S(t)$ 为 $t$ 时所有结点值的和。 定义 $F(A)$ 为树在 $0 \le t \le 10^{100}$ 中所有 $S(t)$ 的和。其中 $A$ 为树在时刻 $0$ 时每个结点的值。 求所有 $2^n$ 个 $F(A)$ 的和。