Friendly Spiders

题意翻译

火星上有一种神秘的电子蜘蛛。 为了研究这种蜘蛛，科学家找来了其中的 $n$ 个，每个蜘蛛有不同的腿数，用数组 $a$ 表示。科学家们发现，有的蜘蛛互相是朋友，如果第 $i$ 个蜘蛛和第 $j$ 个蜘蛛是朋友的话，那么要满足 $\operatorname{gcd}(a_{i},a_{j})≠1$，其中 $\operatorname{gcd}(x,y)$ 函数表示求 $x$ 和 $y$ 的最大公约数。 科学家发现蜘蛛可以互相发送信息。如果两只蜘蛛是朋友，那么它们可以用一秒钟直接发送消息。否则，蜘蛛必须将消息传递给他的朋友，而朋友又必须将消息传递给他的朋友，依此类推，直到消息到达收件人。 假设有一只八条腿的蜘蛛向一只 $15$ 条腿的蜘蛛传递消息，但是由于 $\operatorname{gcd}(8,15)=1$ 所以他不能直接发送，但它可以通过六条腿的蜘蛛发送消息，因为 $\operatorname{gcd}(8,6)=2$ 并且 $\operatorname{gcd}(6,15)=3$ 所以消息将会在两秒钟到达。 目前，科学家们希望找到第 $s$ 个蜘蛛向第 $t$ 个蜘蛛发送消息的最短时间，以及最短路线。 #### 输入 第一行输入一个整数 $n$ $(2\le n \le 3·10^5)$，表示蜘蛛数量。 第二行输入 $n$ 个整数 $a_{1},a_{2},...,a_{n}$ $(1\le a_{i} \le 3·10^5)$，表示蜘蛛的腿数。 第三行包含两个整数 $s$ 和 $t$ $(1\le s,t\le n)$，表示有一条消息需要从第 $s$ 条蜘蛛发给第 $t$ 条蜘蛛。 #### 输出 如果无法在给定的一对蜘蛛之间传输消息，输出 $-1$。 否则，在第一行输出最短时间（单位：秒）。在第二行，输出最短路径，也就是经过传递信息的蜘蛛在 $a$ 数组的位置。按照从发送者到接收者的顺序排列，如果有多个最佳路径，输出其中一个。

题目描述

Mars is home to an unusual species of spiders — Binary spiders. Right now, Martian scientists are observing a colony of $ n $ spiders, the $ i $ -th of which has $ a_i $ legs. Some of the spiders are friends with each other. Namely, the $ i $ -th and $ j $ -th spiders are friends if $ \gcd(a_i, a_j) \ne 1 $ , i. e., there is some integer $ k \ge 2 $ such that $ a_i $ and $ a_j $ are simultaneously divided by $ k $ without a remainder. Here $ \gcd(x, y) $ denotes the [greatest common divisor (GCD)](https://en.wikipedia.org/wiki/Greatest_common_divisor) of integers $ x $ and $ y $ . Scientists have discovered that spiders can send messages. If two spiders are friends, then they can transmit a message directly in one second. Otherwise, the spider must pass the message to his friend, who in turn must pass the message to his friend, and so on until the message reaches the recipient. Let's look at an example. Suppose a spider with eight legs wants to send a message to a spider with $ 15 $ legs. He can't do it directly, because $ \gcd(8, 15) = 1 $ . But he can send a message through the spider with six legs because $ \gcd(8, 6) = 2 $ and $ \gcd(6, 15) = 3 $ . Thus, the message will arrive in two seconds. Right now, scientists are observing how the $ s $ -th spider wants to send a message to the $ t $ -th spider. The researchers have a hypothesis that spiders always transmit messages optimally. For this reason, scientists would need a program that could calculate the minimum time to send a message and also deduce one of the optimal routes.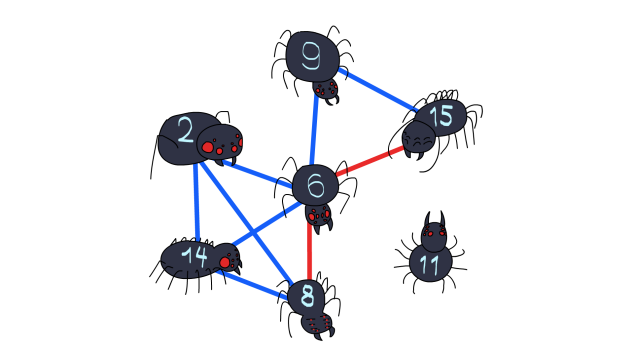 

输入输出格式

输入格式

The first line of input contains an integer $ n $ ( $ 2 \le n \le 3\cdot10^5 $ ) — the number of spiders in the colony. The second line of input contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 3\cdot10^5 $ ) — the number of legs the spiders have. The third line of input contains two integers $ s $ and $ t $ ( $ 1 \le s, t \le n $ ) —the spiders between which the message must be sent.

输出格式

If it is impossible to transmit a message between the given pair of spiders, print $ -1 $ . Otherwise, in the first line of the output print the integer $ t $ ( $ t \ge 1 $ ) — the number of spiders that participate in the message transmission (i. e. the minimum time of message delivery in seconds plus one). In the second line, print $ t $ different integers $ b_1, b_2, \ldots, b_t $ ( $ 1 \le b_i \le n $ ) — the ids of the spiders through which the message should follow, in order from sender to receiver. If there are several optimal routes for the message, output any of them.

输入输出样例

输入样例 #1

7
2 14 9 6 8 15 11
5 6

输出样例 #1

3
5 4 6

输入样例 #2

7
2 14 9 6 8 15 11
5 7

输出样例 #2

-1

输入样例 #3

7
2 14 9 6 8 15 11
5 5

输出样例 #3

1
5

说明

The first example is shown above. It shows that the message from the $ 5 $ -th spider (with eight legs) to the $ 6 $ -th spider (with $ 15 $ legs) is optimal to pass through the $ 4 $ -th spider (with six legs). In the second example, the spider number $ 7 $ (with $ 11 $ legs) is not friends with anyone, so it is impossible to send him a message.

题目大意：
火星上存在一种独特的蜘蛛，科学家们正在研究其中的n只，每只蜘蛛有不同的腿数，用数组a表示。如果两只蜘蛛的最大公约数不等于1，则这两只蜘蛛是朋友。蜘蛛可以通过朋友直接传递信息，如果两只蜘蛛不是朋友，则必须通过其他朋友间接传递，直到信息到达接收者。给定两只蜘蛛，求它们之间传递信息的最短时间和路径。

输入输出数据格式：
输入：
第一行：一个整数n（2≤n≤3·10^5），表示蜘蛛的数量。
第二行：n个整数a_1, a_2, ..., a_n（1≤a_i≤3·10^5），表示每只蜘蛛的腿数。
第三行：两个整数s和t（1≤s,t≤n），表示需要从第s只蜘蛛向第t只蜘蛛传递信息。

输出：
如果无法在给定的一对蜘蛛之间传递消息，输出-1。
否则，第一行输出最短时间（单位：秒）。在第二行，输出最短路径，也就是经过传递信息的蜘蛛在a数组的位置。如果有多个最佳路径，输出其中一个。题目大意： 火星上存在一种独特的蜘蛛，科学家们正在研究其中的n只，每只蜘蛛有不同的腿数，用数组a表示。如果两只蜘蛛的最大公约数不等于1，则这两只蜘蛛是朋友。蜘蛛可以通过朋友直接传递信息，如果两只蜘蛛不是朋友，则必须通过其他朋友间接传递，直到信息到达接收者。给定两只蜘蛛，求它们之间传递信息的最短时间和路径。 输入输出数据格式： 输入： 第一行：一个整数n（2≤n≤3·10^5），表示蜘蛛的数量。 第二行：n个整数a_1, a_2, ..., a_n（1≤a_i≤3·10^5），表示每只蜘蛛的腿数。 第三行：两个整数s和t（1≤s,t≤n），表示需要从第s只蜘蛛向第t只蜘蛛传递信息。 输出： 如果无法在给定的一对蜘蛛之间传递消息，输出-1。 否则，第一行输出最短时间（单位：秒）。在第二行，输出最短路径，也就是经过传递信息的蜘蛛在a数组的位置。如果有多个最佳路径，输出其中一个。