309966: CF1765I. Infinite Chess
Memory Limit:512 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Infinite Chess
题目描述
The black king lives on a chess board with an infinite number of columns (files) and $ 8 $ rows (ranks). The columns are numbered with all integer numbers (including negative). The rows are numbered from $ 1 $ to $ 8 $ . Initially, the black king is located on the starting square $ (x_s, y_s) $ , and he needs to reach some target square $ (x_t, y_t) $ . Unfortunately, there are also white pieces on the board, and they threaten the black king. After negotiations, the white pieces agreed to let the black king pass to the target square on the following conditions: - each turn, the black king makes a move according to the movement rules; - the black king cannot move to a square occupied by a white piece; - the black king cannot move to a square which is under attack by any white piece. A square is under attack if a white piece can reach it in one move according to the movement rules; - the white pieces never move. Help the black king find the minimum number of moves needed to reach the target square while not violating the conditions. The black king cannot leave the board at any time. The black king moves according to the movement rules below. Even though the white pieces never move, squares which they can reach in one move are considered to be under attack, so the black king cannot move into those squares. Below are the movement rules. Note that the pieces (except for the knight) cannot jump over other pieces. - a king moves exactly one square horizontally, vertically, or diagonally. - a rook moves any number of vacant squares horizontally or vertically. - a bishop moves any number of vacant squares diagonally. - a queen moves any number of vacant squares horizontally, vertically, or diagonally. - a knight moves to one of the nearest squares not on the same rank, file, or diagonal (this can be thought of as moving two squares horizontally then one square vertically, or moving one square horizontally then two squares vertically — i. e. in an "L" pattern). Knights are not blocked by other pieces, they can simply jump over them. There are no pawns on the board. 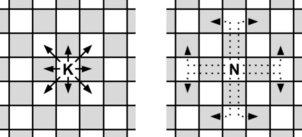 King and knight possible moves, respectively. Dotted line shows that knight can jump over other pieces. 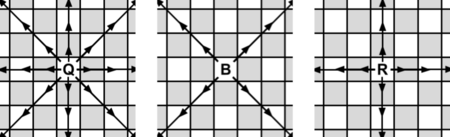 Queen, bishop, and rook possible moves, respectively.输入输出格式
输入格式
The first line contains two integers $ x_s $ and $ y_s $ ( $ 1 \le x_s \le 10^8 $ ; $ 1 \le y_s \le 8 $ ) — the starting coordinates of the black king. The second line contains two integers $ x_t $ and $ y_t $ ( $ 1 \le x_t \le 10^8 $ ; $ 1 \le y_t \le 8 $ ) — the coordinates of the target square for the black king. The third line contains one integer $ n $ ( $ 0 \le n \le 2000 $ ) — the number of white pieces on the board. Then $ n $ lines follow, the $ i $ -th line contains one character $ t_i $ and two integers $ x_i $ and $ y_i $ ( $ 1 \le x_i \le 10^8 $ ; $ 1 \le y_i \le 8 $ ) — the type and the coordinates of the $ i $ -th white piece. The types of pieces are represented by the following uppercase Latin letters: - K — king - Q — queen - R — rook - B — bishop - N — knight There can be any number of white pieces of any type listed above on the board, for example, $ 3 $ white kings or $ 4 $ white queens. There are no pawns on the board. Additional constrains on the input: - no square is occupied by more than one white piece; - the starting square for the black king is different from the square he wants to reach, and neither of these two squares is occupied or is under attack by any white piece.
输出格式
Print one integer — the minimum number of moves needed for the black king to reach the target square while not violating the conditions, or $ -1 $ if it is impossible.
输入输出样例
输入样例 #1
1 8
7 8
2
N 4 8
B 4 6输出样例 #1
10输入样例 #2
1 1
1 5
2
K 1 3
R 2 3输出样例 #2
6输入样例 #3
2 2
6 4
1
Q 4 3输出样例 #3
-1说明
The image below demonstrates the solution for the second example. Here, the letters K, R, s, and t represent the white king, the white rook, the starting square, and the target square, respectively. Bold crosses mark the squares which are under attack by the white pieces. Bold dots show the shortest path for the black king. 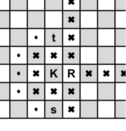Input
题意翻译
一个八行、无数列的棋盘。行的编号为 $1$ 到 $8$ ,列的编号为所有整数 **(包括负数)**。棋盘上有一个黑王和一些白棋。最初黑王位于 $(x_s,y_s)$ ,要到达 $(x_t,y_t)$。 棋子根据以下条件移动: - 每轮黑王根据**移动规则**移动一步。 - 黑王不能移动到被白棋占据的格子。 - 黑王不能移动到**被攻击**的格子。 - 白棋从不移动。 一个格子能被白棋根据**移动规则**用一步移动到,则称该格子“**被攻击**”。 **移动规则**如下(同国际象棋)。 - 王(K)能在水平、竖直或对角线方向移动一格。 - 车(R)能在水平或竖直方向移动任意格。 - 象(B)能在对角线方向移动任意格。 - 后(Q)能在水平、竖直或对角线方向移动任意格。 - 马(N)能移动到不在同一行、列和对角线上的最近的正方形,且不会被其他棋子阻挡(即马走日但不存在蹩马腿)。 - 每个格子最多只能有一个棋子,且除马以外的所有棋子都会被其他棋子挡住。 - 任何棋子不能离开棋盘。 棋盘上每种白棋可以有任意个。棋盘上没有兵。 求黑王在不违反规则的情况下到达终点的最小步数。 输入保证每个格子最多一个棋子、黑王的起点与终点不同且都没有被白棋占据或被攻击。Output
**无尽象棋**
**题目描述:**
黑王生活在一个具有无限列(文件)和8行(等级)的棋盘上。列用所有整数编号(包括负数)。行从1到8编号。
最初,黑王位于起始方格(x_s, y_s),他需要到达某个目标方格(x_t, y_t)。不幸的是,棋盘上还有白棋,它们威胁着黑王。经过谈判,白棋同意让黑王在以下条件下到达目标方格:
- 每一回合,黑王根据移动规则进行移动;
- 黑王不能移动到有白棋的方格;
- 黑王不能移动到任何白棋攻击的方格。如果一个白棋可以在一步内根据移动规则到达一个方格,则该方格受到攻击;
- 白棋永不移动。
帮助黑王找到在不违反条件的情况下到达目标方格所需的最小移动次数。黑王不能在任何时间离开棋盘。
黑王根据以下移动规则移动。尽管白棋从不移动,但它们可以在一步内到达的方格被认为受到攻击,因此黑王不能移动到那些方格。
以下是移动规则。注意,除了马之外,棋子不能跳过其他棋子。
- 王每次移动一格,可以水平、垂直或对角线方向。
- 车可以水平或垂直方向移动任意数量的空格。
- 象可以沿对角线方向移动任意数量的空格。
- 后可以水平、垂直或对角线方向移动任意数量的空格。
- 马移动到最近的、不在同一行、列或对角线上的方格之一(这可以认为是先水平移动两格然后垂直移动一格,或者先水平移动一格然后垂直移动两格——即“L”形图案)。马不受其他棋子阻挡,它们可以简单地跳过它们。
棋盘上没有兵。
**输入输出格式:**
**输入格式:**
第一行包含两个整数$ x_s $和$ y_s $($ 1 \le x_s \le 10^8 $;$ 1 \le y_s \le 8 $)——黑王的起始坐标。
第二行包含两个整数$ x_t $和$ y_t $($ 1 \le x_t \le 10^8 $;$ 1 \le y_t \le 8 $)——黑王的目标方格坐标。
第三行包含一个整数$ n $($ 0 \le n \le 2000 $)——棋盘上的白棋数量。
然后是$ n $行,第$ i $行包含一个字符$ t_i $和两个整数$ x_i $和$ y_i $($ 1 \le x_i \le 10^8 $;$ 1 \le y_i \le 8 $)——第$ i $个白棋的类型和坐标。棋子类型由以下大写拉丁字母表示:
- K —— 王
- Q —— 后
- R —— 车
- B —— 象
- N —— 马
棋盘上可以有任意数量的上述任何类型的白棋,例如,3个白王或4个白后。棋盘上没有兵。
输入的附加限制:
- 没有一个方格被多于一个白棋占据;
- 黑王的起始方格与他想到达的方格不同,且这两个方格均未被占据或被任何白棋攻击。
**输出格式:**
打印一个整数——黑王在不违反条件的情况下到达目标方格所需的最小移动次数,或如果不可能则为-1。
**输入输出样例:**
**输入样例 #1:**
```
1 8
7 8
2
N 4 8
B 4 6
```
**输出样例 #1:**
```
10
```
**输入样例 #2:**
```
1 1
1 5
2
K 1 3
R 2 3
```
**输出样例 #2:**
```
6
```
**输入样例 #3:**
```
2 2
6 4
1
Q 4 3
```
**输出样例 #3:**
```
-1
```
**说明:**
下面的图像展示了第二个示例的解决方案。这里,字母K、R、s和t分别代表白王、白车、起始方格和目标方格。粗十字标记被白棋攻击的方格。粗点显示黑王的最短路径。**无尽象棋** **题目描述:** 黑王生活在一个具有无限列(文件)和8行(等级)的棋盘上。列用所有整数编号(包括负数)。行从1到8编号。 最初,黑王位于起始方格(x_s, y_s),他需要到达某个目标方格(x_t, y_t)。不幸的是,棋盘上还有白棋,它们威胁着黑王。经过谈判,白棋同意让黑王在以下条件下到达目标方格: - 每一回合,黑王根据移动规则进行移动; - 黑王不能移动到有白棋的方格; - 黑王不能移动到任何白棋攻击的方格。如果一个白棋可以在一步内根据移动规则到达一个方格,则该方格受到攻击; - 白棋永不移动。 帮助黑王找到在不违反条件的情况下到达目标方格所需的最小移动次数。黑王不能在任何时间离开棋盘。 黑王根据以下移动规则移动。尽管白棋从不移动,但它们可以在一步内到达的方格被认为受到攻击,因此黑王不能移动到那些方格。 以下是移动规则。注意,除了马之外,棋子不能跳过其他棋子。 - 王每次移动一格,可以水平、垂直或对角线方向。 - 车可以水平或垂直方向移动任意数量的空格。 - 象可以沿对角线方向移动任意数量的空格。 - 后可以水平、垂直或对角线方向移动任意数量的空格。 - 马移动到最近的、不在同一行、列或对角线上的方格之一(这可以认为是先水平移动两格然后垂直移动一格,或者先水平移动一格然后垂直移动两格——即“L”形图案)。马不受其他棋子阻挡,它们可以简单地跳过它们。 棋盘上没有兵。 **输入输出格式:** **输入格式:** 第一行包含两个整数$ x_s $和$ y_s $($ 1 \le x_s \le 10^8 $;$ 1 \le y_s \le 8 $)——黑王的起始坐标。 第二行包含两个整数$ x_t $和$ y_t $($ 1 \le x_t \le 10^8 $;$ 1 \le y_t \le 8 $)——黑王的目标方格坐标。 第三行包含一个整数$ n $($ 0 \le n \le 2000 $)——棋盘上的白棋数量。 然后是$ n $行,第$ i $行包含一个字符$ t_i $和两个整数$ x_i $和$ y_i $($ 1 \le x_i \le 10^8 $;$ 1 \le y_i \le 8 $)——第$ i $个白棋的类型和坐标。棋子类型由以下大写拉丁字母表示: - K —— 王 - Q —— 后 - R —— 车 - B —— 象 - N —— 马 棋盘上可以有任意数量的上述任何类型的白棋,例如,3个白王或4个白后。棋盘上没有兵。 输入的附加限制: - 没有一个方格被多于一个白棋占据; - 黑王的起始方格与他想到达的方格不同,且这两个方格均未被占据或被任何白棋攻击。 **输出格式:** 打印一个整数——黑王在不违反条件的情况下到达目标方格所需的最小移动次数,或如果不可能则为-1。 **输入输出样例:** **输入样例 #1:** ``` 1 8 7 8 2 N 4 8 B 4 6 ``` **输出样例 #1:** ``` 10 ``` **输入样例 #2:** ``` 1 1 1 5 2 K 1 3 R 2 3 ``` **输出样例 #2:** ``` 6 ``` **输入样例 #3:** ``` 2 2 6 4 1 Q 4 3 ``` **输出样例 #3:** ``` -1 ``` **说明:** 下面的图像展示了第二个示例的解决方案。这里,字母K、R、s和t分别代表白王、白车、起始方格和目标方格。粗十字标记被白棋攻击的方格。粗点显示黑王的最短路径。
**题目描述:**
黑王生活在一个具有无限列(文件)和8行(等级)的棋盘上。列用所有整数编号(包括负数)。行从1到8编号。
最初,黑王位于起始方格(x_s, y_s),他需要到达某个目标方格(x_t, y_t)。不幸的是,棋盘上还有白棋,它们威胁着黑王。经过谈判,白棋同意让黑王在以下条件下到达目标方格:
- 每一回合,黑王根据移动规则进行移动;
- 黑王不能移动到有白棋的方格;
- 黑王不能移动到任何白棋攻击的方格。如果一个白棋可以在一步内根据移动规则到达一个方格,则该方格受到攻击;
- 白棋永不移动。
帮助黑王找到在不违反条件的情况下到达目标方格所需的最小移动次数。黑王不能在任何时间离开棋盘。
黑王根据以下移动规则移动。尽管白棋从不移动,但它们可以在一步内到达的方格被认为受到攻击,因此黑王不能移动到那些方格。
以下是移动规则。注意,除了马之外,棋子不能跳过其他棋子。
- 王每次移动一格,可以水平、垂直或对角线方向。
- 车可以水平或垂直方向移动任意数量的空格。
- 象可以沿对角线方向移动任意数量的空格。
- 后可以水平、垂直或对角线方向移动任意数量的空格。
- 马移动到最近的、不在同一行、列或对角线上的方格之一(这可以认为是先水平移动两格然后垂直移动一格,或者先水平移动一格然后垂直移动两格——即“L”形图案)。马不受其他棋子阻挡,它们可以简单地跳过它们。
棋盘上没有兵。
**输入输出格式:**
**输入格式:**
第一行包含两个整数$ x_s $和$ y_s $($ 1 \le x_s \le 10^8 $;$ 1 \le y_s \le 8 $)——黑王的起始坐标。
第二行包含两个整数$ x_t $和$ y_t $($ 1 \le x_t \le 10^8 $;$ 1 \le y_t \le 8 $)——黑王的目标方格坐标。
第三行包含一个整数$ n $($ 0 \le n \le 2000 $)——棋盘上的白棋数量。
然后是$ n $行,第$ i $行包含一个字符$ t_i $和两个整数$ x_i $和$ y_i $($ 1 \le x_i \le 10^8 $;$ 1 \le y_i \le 8 $)——第$ i $个白棋的类型和坐标。棋子类型由以下大写拉丁字母表示:
- K —— 王
- Q —— 后
- R —— 车
- B —— 象
- N —— 马
棋盘上可以有任意数量的上述任何类型的白棋,例如,3个白王或4个白后。棋盘上没有兵。
输入的附加限制:
- 没有一个方格被多于一个白棋占据;
- 黑王的起始方格与他想到达的方格不同,且这两个方格均未被占据或被任何白棋攻击。
**输出格式:**
打印一个整数——黑王在不违反条件的情况下到达目标方格所需的最小移动次数,或如果不可能则为-1。
**输入输出样例:**
**输入样例 #1:**
```
1 8
7 8
2
N 4 8
B 4 6
```
**输出样例 #1:**
```
10
```
**输入样例 #2:**
```
1 1
1 5
2
K 1 3
R 2 3
```
**输出样例 #2:**
```
6
```
**输入样例 #3:**
```
2 2
6 4
1
Q 4 3
```
**输出样例 #3:**
```
-1
```
**说明:**
下面的图像展示了第二个示例的解决方案。这里,字母K、R、s和t分别代表白王、白车、起始方格和目标方格。粗十字标记被白棋攻击的方格。粗点显示黑王的最短路径。**无尽象棋** **题目描述:** 黑王生活在一个具有无限列(文件)和8行(等级)的棋盘上。列用所有整数编号(包括负数)。行从1到8编号。 最初,黑王位于起始方格(x_s, y_s),他需要到达某个目标方格(x_t, y_t)。不幸的是,棋盘上还有白棋,它们威胁着黑王。经过谈判,白棋同意让黑王在以下条件下到达目标方格: - 每一回合,黑王根据移动规则进行移动; - 黑王不能移动到有白棋的方格; - 黑王不能移动到任何白棋攻击的方格。如果一个白棋可以在一步内根据移动规则到达一个方格,则该方格受到攻击; - 白棋永不移动。 帮助黑王找到在不违反条件的情况下到达目标方格所需的最小移动次数。黑王不能在任何时间离开棋盘。 黑王根据以下移动规则移动。尽管白棋从不移动,但它们可以在一步内到达的方格被认为受到攻击,因此黑王不能移动到那些方格。 以下是移动规则。注意,除了马之外,棋子不能跳过其他棋子。 - 王每次移动一格,可以水平、垂直或对角线方向。 - 车可以水平或垂直方向移动任意数量的空格。 - 象可以沿对角线方向移动任意数量的空格。 - 后可以水平、垂直或对角线方向移动任意数量的空格。 - 马移动到最近的、不在同一行、列或对角线上的方格之一(这可以认为是先水平移动两格然后垂直移动一格,或者先水平移动一格然后垂直移动两格——即“L”形图案)。马不受其他棋子阻挡,它们可以简单地跳过它们。 棋盘上没有兵。 **输入输出格式:** **输入格式:** 第一行包含两个整数$ x_s $和$ y_s $($ 1 \le x_s \le 10^8 $;$ 1 \le y_s \le 8 $)——黑王的起始坐标。 第二行包含两个整数$ x_t $和$ y_t $($ 1 \le x_t \le 10^8 $;$ 1 \le y_t \le 8 $)——黑王的目标方格坐标。 第三行包含一个整数$ n $($ 0 \le n \le 2000 $)——棋盘上的白棋数量。 然后是$ n $行,第$ i $行包含一个字符$ t_i $和两个整数$ x_i $和$ y_i $($ 1 \le x_i \le 10^8 $;$ 1 \le y_i \le 8 $)——第$ i $个白棋的类型和坐标。棋子类型由以下大写拉丁字母表示: - K —— 王 - Q —— 后 - R —— 车 - B —— 象 - N —— 马 棋盘上可以有任意数量的上述任何类型的白棋,例如,3个白王或4个白后。棋盘上没有兵。 输入的附加限制: - 没有一个方格被多于一个白棋占据; - 黑王的起始方格与他想到达的方格不同,且这两个方格均未被占据或被任何白棋攻击。 **输出格式:** 打印一个整数——黑王在不违反条件的情况下到达目标方格所需的最小移动次数,或如果不可能则为-1。 **输入输出样例:** **输入样例 #1:** ``` 1 8 7 8 2 N 4 8 B 4 6 ``` **输出样例 #1:** ``` 10 ``` **输入样例 #2:** ``` 1 1 1 5 2 K 1 3 R 2 3 ``` **输出样例 #2:** ``` 6 ``` **输入样例 #3:** ``` 2 2 6 4 1 Q 4 3 ``` **输出样例 #3:** ``` -1 ``` **说明:** 下面的图像展示了第二个示例的解决方案。这里,字母K、R、s和t分别代表白王、白车、起始方格和目标方格。粗十字标记被白棋攻击的方格。粗点显示黑王的最短路径。