Hanging Hearts

题意翻译

你有 $ n $ 张心形卡片，第 $ 1 $ 张卡片被直接贴在墙上。 除此之外，第 $ i $ ( $ i > 1 $ ) 张卡片被一根绳子挂在第 $ p_i $ ( $ p_i < i $ ) 张卡片上。 第 $i$ 张卡片上写着一个数字 $ a_i $ 。 初始时你可以将数组 $ a $ 设置为 $ [1, 2, \dots, n] $ 的**任意**一个排列。接下来进行 $ n $ 次如下操作，并维护一个数列 $ s $（初始为空）： 1. 选择一张卡片 $ x $ ，使得没有其他卡片挂在 $ x $ 上； 2. 将卡片 $ x $ 上的数字添加到 $ s $ 的末尾； 3. 如果 $ x \neq 1 $ ，且 $ p_x $ 上的数字大于 $ x $ 上的数字，则交换两卡片的数字； 4. 移除卡片 $ x $。 求 $ n $ 次操作后，$ s $ 的最长不下降子序列长度**最大**是多少。

题目描述

Pak Chanek has $ n $ blank heart-shaped cards. Card $ 1 $ is attached directly to the wall while each of the other cards is hanging onto exactly one other card by a piece of string. Specifically, card $ i $ ( $ i > 1 $ ) is hanging onto card $ p_i $ ( $ p_i < i $ ). In the very beginning, Pak Chanek must write one integer number on each card. He does this by choosing any permutation $ a $ of $ [1, 2, \dots, n] $ . Then, the number written on card $ i $ is $ a_i $ . After that, Pak Chanek must do the following operation $ n $ times while maintaining a sequence $ s $ (which is initially empty): 1. Choose a card $ x $ such that no other cards are hanging onto it. 2. Append the number written on card $ x $ to the end of $ s $ . 3. If $ x \neq 1 $ and the number on card $ p_x $ is larger than the number on card $ x $ , replace the number on card $ p_x $ with the number on card $ x $ . 4. Remove card $ x $ . After that, Pak Chanek will have a sequence $ s $ with $ n $ elements. What is the maximum length of the longest non-decreasing subsequence $ ^\dagger $ of $ s $ at the end if Pak Chanek does all the steps optimally? $ ^\dagger $ A sequence $ b $ is a subsequence of a sequence $ c $ if $ b $ can be obtained from $ c $ by deletion of several (possibly, zero or all) elements. For example, $ [3,1] $ is a subsequence of $ [3,2,1] $ , $ [4,3,1] $ and $ [3,1] $ , but not $ [1,3,3,7] $ and $ [3,10,4] $ .

输入输出格式

输入格式

The first line contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of heart-shaped cards. The second line contains $ n - 1 $ integers $ p_2, p_3, \dots, p_n $ ( $ 1 \le p_i < i $ ) describing which card that each card hangs onto.

输出格式

Print a single integer — the maximum length of the longest non-decreasing subsequence of $ s $ at the end if Pak Chanek does all the steps optimally.

输入输出样例

输入样例 #1

6
1 2 1 4 2

输出样例 #1

4

输入样例 #2

2
1

输出样例 #2

2

说明

The following is the structure of the cards in the first example. 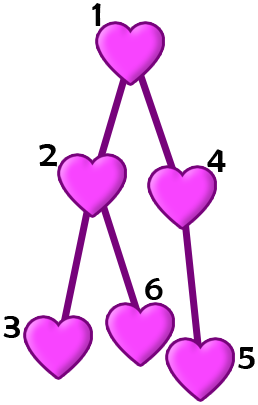 Pak Chanek can choose the permutation $ a = [1, 5, 4, 3, 2, 6] $ .  Let $ w_i $ be the number written on card $ i $ . Initially, $ w_i = a_i $ . Pak Chanek can do the following operations in order: 1. Select card $ 5 $ . Append $ w_5 = 2 $ to the end of $ s $ . As $ w_4 > w_5 $ , the value of $ w_4 $ becomes $ 2 $ . Remove card $ 5 $ . After this operation, $ s = [2] $ . 2. Select card $ 6 $ . Append $ w_6 = 6 $ to the end of $ s $ . As $ w_2 \leq w_6 $ , the value of $ w_2 $ is left unchanged. Remove card $ 6 $ . After this operation, $ s = [2, 6] $ . 3. Select card $ 4 $ . Append $ w_4 = 2 $ to the end of $ s $ . As $ w_1 \leq w_4 $ , the value of $ w_1 $ is left unchanged. Remove card $ 4 $ . After this operation, $ s = [2, 6, 2] $ . 4. Select card $ 3 $ . Append $ w_3 = 4 $ to the end of $ s $ . As $ w_2 > w_3 $ , the value of $ w_2 $ becomes $ 4 $ . Remove card $ 3 $ . After this operation, $ s = [2, 6, 2, 4] $ . 5. Select card $ 2 $ . Append $ w_2 = 4 $ to the end of $ s $ . As $ w_1 \leq w_2 $ , the value of $ w_1 $ is left unchanged. Remove card $ 2 $ . After this operation, $ s = [2, 6, 2, 4, 4] $ . 6. Select card $ 1 $ . Append $ w_1 = 1 $ to the end of $ s $ . Remove card $ 1 $ . After this operation, $ s = [2, 6, 2, 4, 4, 1] $ . One of the longest non-decreasing subsequences of $ s = [2, 6, 2, 4, 4, 1] $ is $ [2, 2, 4, 4] $ . Thus, the length of the longest non-decreasing subsequence of $ s $ is $ 4 $ . It can be proven that this is indeed the maximum possible length.

**题目大意：**

Pak Chanek有 $ n $ 张心形空白卡片。第 $ 1 $ 张卡片直接贴在墙上，而其他的每张卡片都通过一条绳子挂在前一张卡片上。具体来说，第 $ i $ 张卡片（$ i > 1 $）挂在第 $ p_i $ 张卡片（$ p_i < i $）上。

一开始，Pak Chanek可以在每张卡片上写一个整数。他通过选择 $ [1, 2, \dots, n] $ 的任意排列 $ a $ 来做到这一点。那么，第 $ i $ 张卡片上写的数字就是 $ a_i $。

之后，Pak Chanek必须执行以下操作 $ n $ 次，同时维护一个序列 $ s $（最初为空）：

1. 选择一张卡片 $ x $，使得没有其他卡片挂在 $ x $ 上；
2. 将卡片 $ x $ 上的数字添加到 $ s $ 的末尾；
3. 如果 $ x \neq 1 $ 且 $ p_x $ 上的数字大于 $ x $ 上的数字，则交换两个卡片上的数字；
4. 移除卡片 $ x $。

操作结束后，Pak Chanek将得到一个包含 $ n $ 个元素的序列 $ s $。如果Pak Chanek的所有步骤都是最优的，那么最后 $ s $ 的最长不下降子序列的最大长度是多少？

**输入输出数据格式：**

- **输入格式：**
- 第一行包含一个整数 $ n $（$ 2 \le n \le 10^5 $）——心形卡片的总数。
- 第二行包含 $ n - 1 $ 个整数 $ p_2, p_3, \dots, p_n $（$ 1 \le p_i < i $），描述每张卡片挂在哪张卡片上。

- **输出格式：**
- 打印一个整数——如果Pak Chanek的所有步骤都是最优的，那么最后 $ s $ 的最长不下降子序列的最大长度是多少。

**输入输出样例：**

- **输入样例 #1：**
```
6
1 2 1 4 2
```
- **输出样例 #1：**
```
4
```

- **输入样例 #2：**
```
2
1
```
- **输出样例 #2：**
```
2
```**题目大意：** Pak Chanek有 $ n $ 张心形空白卡片。第 $ 1 $ 张卡片直接贴在墙上，而其他的每张卡片都通过一条绳子挂在前一张卡片上。具体来说，第 $ i $ 张卡片（$ i > 1 $）挂在第 $ p_i $ 张卡片（$ p_i < i $）上。 一开始，Pak Chanek可以在每张卡片上写一个整数。他通过选择 $ [1, 2, \dots, n] $ 的任意排列 $ a $ 来做到这一点。那么，第 $ i $ 张卡片上写的数字就是 $ a_i $。 之后，Pak Chanek必须执行以下操作 $ n $ 次，同时维护一个序列 $ s $（最初为空）： 1. 选择一张卡片 $ x $，使得没有其他卡片挂在 $ x $ 上； 2. 将卡片 $ x $ 上的数字添加到 $ s $ 的末尾； 3. 如果 $ x \neq 1 $ 且 $ p_x $ 上的数字大于 $ x $ 上的数字，则交换两个卡片上的数字； 4. 移除卡片 $ x $。 操作结束后，Pak Chanek将得到一个包含 $ n $ 个元素的序列 $ s $。如果Pak Chanek的所有步骤都是最优的，那么最后 $ s $ 的最长不下降子序列的最大长度是多少？ **输入输出数据格式：** - **输入格式：** - 第一行包含一个整数 $ n $（$ 2 \le n \le 10^5 $）——心形卡片的总数。 - 第二行包含 $ n - 1 $ 个整数 $ p_2, p_3, \dots, p_n $（$ 1 \le p_i < i $），描述每张卡片挂在哪张卡片上。 - **输出格式：** - 打印一个整数——如果Pak Chanek的所有步骤都是最优的，那么最后 $ s $ 的最长不下降子序列的最大长度是多少。 **输入输出样例：** - **输入样例 #1：** ``` 6 1 2 1 4 2 ``` - **输出样例 #1：** ``` 4 ``` - **输入样例 #2：** ``` 2 1 ``` - **输出样例 #2：** ``` 2 ```