Jumbo Extra Cheese 2

题意翻译

给定 $n$ 个矩形，第 $i$ 个矩形表示为 $a_i \times b_i$。 现在你要将这些矩形放在一个平面直角坐标系中，满足以下条件： 1. 每个矩形均有一条边在 x 轴上； 2. 保证这些矩形互不相交，且从左到右**两两相切**。 你可以将这些矩形以任意顺序排列，任意方向旋转，但必须保证满足以上条件。 求出所有矩形所**组成图形**的最小周长。

题目描述

Pak Chanek has $ n $ two-dimensional slices of cheese. The $ i $ -th slice of cheese can be represented as a rectangle of dimensions $ a_i \times b_i $ . We want to arrange them on the two-dimensional plane such that: - Each edge of each cheese is parallel to either the x-axis or the y-axis. - The bottom edge of each cheese is a segment of the x-axis. - No two slices of cheese overlap, but their sides can touch. - They form one connected shape. Note that we can arrange them in any order (the leftmost slice of cheese is not necessarily the first slice of cheese). Also note that we can rotate each slice of cheese in any way as long as all conditions still hold. Find the minimum possible perimeter of the constructed shape.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains an integer $ t $ ( $ 1 \leq t \leq 2 \cdot 10^4 $ ) — the number of test cases. The following lines contain the description of each test case. The first line of each test case contains an integer $ n $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ ) — the number of slices of cheese Pak Chanek has. The $ i $ -th of the next $ n $ lines of each test case contains two integers $ a_i $ and $ b_i $ ( $ 1 \leq a_i,b_i \leq 10^9 $ ) — the dimensions of the $ i $ -th slice of cheese. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, output a line containing an integer representing the minimum possible perimeter of the constructed shape.

输入输出样例

输入样例 #1

3
4
4 1
4 5
1 1
2 3
3
2 4
2 6
2 3
1
2 65

输出样例 #1

26
24
134

说明

In the first test case, a way of getting the minimum possible perimeter is to arrange the slices of cheese as follows.  We can calculate that the perimeter of the constructed shape is $ 2+5+1+1+1+1+3+1+5+1+2+3=26 $ . It can be shown that we cannot get a smaller perimeter. Consider the following invalid arrangement. 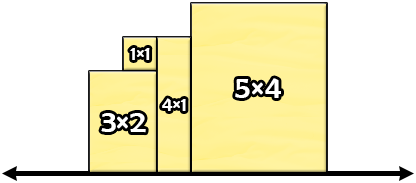 Even though the perimeter of the shape above is $ 24 $ , it does not satisfy all conditions of the problem. The bottom edge of the $ 1 \times 1 $ slice of cheese is not a segment of the x-axis. In the second test case, a way of getting the minimum possible perimeter is to arrange the slices of cheese as follows. 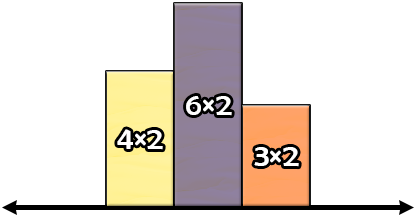 We can calculate that the perimeter of the constructed shape is $ 2+2+2+3+2+3+2+2+2+4=24 $ . It can be shown that we cannot get a smaller perimeter.

**题目大意**：

给定 $n$ 个矩形，第 $i$ 个矩形的长和宽分别为 $a_i$ 和 $b_i$。需要将这些矩形放置在一个平面直角坐标系中，满足以下条件：

1. 每个矩形至少有一条边与 x 轴平行；
2. 保证这些矩形互不相交，且从左到右相邻矩形的边是相切的；
3. 可以任意顺序排列和旋转这些矩形。

求出所有矩形组成图形的最小周长。

**输入输出数据格式**：

**输入格式**：
- 第一行包含一个整数 $t$（$1 \leq t \leq 2 \cdot 10^4$），表示测试用例的数量。
- 每个测试用例的第一行包含一个整数 $n$（$1 \leq n \leq 2 \cdot 10^5$），表示矩形的数量。
- 接下来的 $n$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq 10^9$），表示第 $i$ 个矩形的长和宽。
- 所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

**输出格式**：
- 对于每个测试用例，输出一行，包含一个整数，表示所构造形状的最小可能周长。

**输入输出样例**：

**输入样例 #1**：
```
3
4
4 1
4 5
1 1
2 3
3
2 4
2 6
2 3
1
2 65
```

**输出样例 #1**：
```
26
24
134
```**题目大意**： 给定 $n$ 个矩形，第 $i$ 个矩形的长和宽分别为 $a_i$ 和 $b_i$。需要将这些矩形放置在一个平面直角坐标系中，满足以下条件： 1. 每个矩形至少有一条边与 x 轴平行； 2. 保证这些矩形互不相交，且从左到右相邻矩形的边是相切的； 3. 可以任意顺序排列和旋转这些矩形。 求出所有矩形组成图形的最小周长。 **输入输出数据格式**： **输入格式**： - 第一行包含一个整数 $t$（$1 \leq t \leq 2 \cdot 10^4$），表示测试用例的数量。 - 每个测试用例的第一行包含一个整数 $n$（$1 \leq n \leq 2 \cdot 10^5$），表示矩形的数量。 - 接下来的 $n$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq 10^9$），表示第 $i$ 个矩形的长和宽。 - 所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。 **输出格式**： - 对于每个测试用例，输出一行，包含一个整数，表示所构造形状的最小可能周长。 **输入输出样例**： **输入样例 #1**： ``` 3 4 4 1 4 5 1 1 2 3 3 2 4 2 6 2 3 1 2 65 ``` **输出样例 #1**： ``` 26 24 134 ```