Field Photography

题意翻译

## 题目描述 PC 正在前往马纳多。原来，2019年印度尼西亚国家科学奥林匹克运动会正在举行。OSN 2019的参赛者目前正在一个待拍照的场地排队。该场地的形状类似于一个大小为 $N\times 10^{100}$ 的网格，有$N$行和$10^{100}$列。行从北到南从 $1$ 编号到 $N$ ，列从西到东从 $1$ 编号到 $10^{100}$ 。第 $r$ 行第 $c$ 列的方格坐标为$(r,c)$。 有 $N$ 个省份参加 OSN 2019。最初，代表省 $i$ 的每个参赛者都会站在方格$（i，p）$中，并满足 $L_i\leq p\leq R_i$ 。因此，我们可以看到有 $R_i-L_i+1$ 个参赛者代表省 $i$ 。 PC 的变量 $Z$ 最初等于 $0$ 。在一次操作中，PC 可以选择行 $i$ 和正整数 $k$ 。然后，PC 将执行以下两种操作之一： - 将第 $i$ 行中的所有参赛者向西移动 $k$ 个方格。换句话说，在 $(i,p)$ 中的选手被移动到 $(i,p-k)$。 - 将第 $i$ 行中的所有参赛者向东移动 $k$ 个方格。换句话说，在 $(i,p)$ 中的选手被移动到 $(i,p+k)$。 每次操作后，$Z$的值将变为$Z~\text{OR}~k$，其中$\text{OR}$是按位或运算. 请注意，PC 可以多次对同一行执行操作。还要注意，PC 不允许将参赛者移出网格。 有 $Q$ 问题。对于第 $j$ 个问题，您将得到一个正整数 $W_j $，PC 必须执行零或更多操作，以便 $Z$ 的最终值正好是 $W_j$ 。将 $M$ 定义为最大的数字，以便在所有操作之后，至少有一列正好包含 $M$ 参赛者。对于每个问题，您必须找到 PC 可以完成的所有操作序列的最大可能 $M$ 。请注意，PC 针对一个问题所做的操作不会延续到其他问题。 ## 输入格式 第一行包含一个整数$N(1\leq N\leq 10^5)~~$ 即网格中的行数以及参与 OSN 2019 的省份数。 接下来 $N$ 行的第 $i$ 行包含两个整数 $L_i$ 和 $R_i~~(1\leq L_i\leq R_i\leq 10^9)$ ，描述代表省 $i$ 的参赛者的位置。 下一行包含将询问的问题数 $Q$（$1\leq Q\leq 10^5$）。 接下来 $Q$ 行的第 $j$ -行包含一个整数$W_j$（$1\leq W_j\leq 10^9$）即第$j$个问题所需的最终值$Z$。 ## 输出格式 输出 $Q$ 行，第 $j$ 行包含一个整数，即第 $j$ 个问题中 $M$ 的最大值。 ## 提示 对于第 $1$ 个问题，PC 可以执行以下操作以获得 $M=2$： - 将第 $2$ 排中的所有参赛者向东移动 $4$ 块 $Z$ 变为$0~\text{OR}~4=4$。 - 将第 $1$ 排中的所有参赛者向东移动$12$块$Z$变为$4~\text{OR}~12=12$。 现在，每列 $14$ 和 $15$ 正好包含 $2$ 的参赛者。 对于第二个 $2$ 问题，PC可以执行以下操作以获得 $M=3$： - 将第 $3$ 排中的所有参赛者向东移动 $4$ 块 $Z$ 变为$0~\text{OR}~4=4$。 - 将第 $3$ 排中的所有参赛者向西移动 $1$ 行 $Z$ 变为 $4~\text{OR}~1=5$。 - 将 $1$ 排中的所有参赛者向东移动$5$块$Z$变为$5~\text{OR}~5=5$。 - 将 $1$ 排中的所有参赛者向东移动 $5$ 块 $Z$ 变为 $5~\text {OR}~5=5$。 现在，第 $11$ 列正好包含 $3$ 名参赛者。 下面是第 $2$ 个问题的示例操作说明。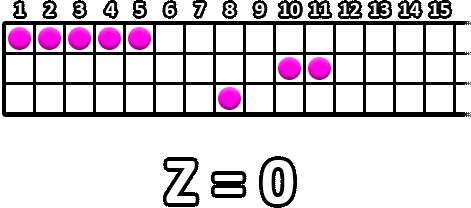 

题目描述

Pak Chanek is traveling to Manado. It turns out that OSN (Indonesian National Scientific Olympiad) 2019 is being held. The contestants of OSN 2019 are currently lining up in a field to be photographed. The field is shaped like a grid of size $ N \times 10^{100} $ with $ N $ rows and $ 10^{100} $ columns. The rows are numbered from $ 1 $ to $ N $ from north to south, the columns are numbered from $ 1 $ to $ 10^{100} $ from west to east. The tile in row $ r $ and column $ c $ is denoted as $ (r,c) $ . There are $ N $ provinces that participate in OSN 2019. Initially, each contestant who represents province $ i $ stands in tile $ (i, p) $ for each $ p $ satisfying $ L_i \leq p \leq R_i $ . So, we can see that there are $ R_i-L_i+1 $ contestants who represent province $ i $ . Pak Chanek has a variable $ Z $ that is initially equal to $ 0 $ . In one operation, Pak Chanek can choose a row $ i $ and a positive integer $ k $ . Then, Pak Chanek will do one of the two following possibilities: - Move all contestants in row $ i $ exactly $ k $ tiles to the west. In other words, a contestant who is in $ (i, p) $ is moved to $ (i, p-k) $ . - Move all contestants in row $ i $ exactly $ k $ tiles to the east. In other words, a contestant who is in $ (i, p) $ is moved to $ (i, p+k) $ . After each operation, the value of $ Z $ will change into $ Z \text{ OR } k $ , with $ \text{OR} $ being the [bitwise OR operation](https://en.wikipedia.org/wiki/Bitwise_operation#OR). Note that Pak Chanek can do operations to the same row more than once. Also note that Pak Chanek is not allowed to move contestants out of the grid. There are $ Q $ questions. For the $ j $ -th question, you are given a positive integer $ W_j $ , Pak Chanek must do zero or more operations so that the final value of $ Z $ is exactly $ W_j $ . Define $ M $ as the biggest number such that after all operations, there is at least one column that contains exactly $ M $ contestants. For each question, you must find the biggest possible $ M $ for all sequences of operations that can be done by Pak Chanek. Note that the operations done by Pak Chanek for one question do not carry over to other questions.

输入输出格式

输入格式

The first line contains a single integer $ N $ ( $ 1 \leq N \leq 10^5 $ ) — the number of rows in the grid and also the number of provinces that participate in OSN 2019. The $ i $ -th of the next $ N $ lines contains two integers $ L_i $ and $ R_i $ ( $ 1 \leq L_i \leq R_i \leq 10^9 $ ) describing the positions of the contestants who represent province $ i $ . The next line contains a single integer $ Q $ ( $ 1 \leq Q \leq 10^5 $ ) — the number of questions. The $ j $ -th of the next $ Q $ lines contains a single integer $ W_j $ ( $ 1 \leq W_j \leq 10^9 $ ) — the required final value of $ Z $ for the $ j $ -th question.

输出格式

Output $ Q $ lines, with the $ j $ -th line containing an integer that is the answer to the $ j $ -th question.

输入输出样例

输入样例 #1

3
1 5
10 11
8 8
2
12
5

输出样例 #1

2
3

说明

For the $ 1 $ -st question, Pak Chanek can do the following operations to get $ M=2 $ : - Move all contestants in row $ 2 $ to the east by $ 4 $ tiles. $ Z $ changes into $ 0 \text{ OR } 4 = 4 $ . - Move all contestants in row $ 1 $ to the east by $ 12 $ tiles. $ Z $ changes into $ 4 \text{ OR } 12 = 12 $ . Now, columns $ 14 $ and $ 15 $ each contains exactly $ 2 $ contestants. For the $ 2 $ -nd question, Pak Chanek can do the following operations to get $ M=3 $ : - Move all contestants in row $ 3 $ to the east by $ 4 $ tiles. $ Z $ changes into $ 0 \text{ OR } 4 = 4 $ . - Move all contestants in row $ 3 $ to the west by $ 1 $ tiles. $ Z $ changes into $ 4 \text{ OR } 1 = 5 $ . - Move all contestants in row $ 1 $ to the east by $ 5 $ tiles. $ Z $ changes into $ 5 \text{ OR } 5 = 5 $ . - Move all contestants in row $ 1 $ to the east by $ 5 $ tiles. $ Z $ changes into $ 5 \text{ OR } 5 = 5 $ . Now, column $ 11 $ contains exactly $ 3 $ contestants. The following is an illustration of the example operations for the $ 2 $ -nd question. 

**题目大意：**

PC正在前往马纳多。原来，2019年印度尼西亚国家科学奥林匹克运动会正在举行。OSN 2019的参赛者目前正在一个待拍照的场地排队。该场地的形状类似于一个大小为$N\times 10^{100}$的网格，有$N$行和$10^{100}$列。行从北到南从$1$编号到$N$，列从西到东从$1$编号到$10^{100}$。第$r$行第$c$列的方格坐标为$(r,c)$。

有$N$个省份参加OSN 2019。最初，代表省$i$的每个参赛者都会站在方格$(i,p)$中，并满足$L_i\leq p\leq R_i$。因此，我们可以看到有$R_i-L_i+1$个参赛者代表省$i$。

PC的变量$Z$最初等于$0$。在一次操作中，PC可以选择行$i$和正整数$k$。然后，PC将执行以下两种操作之一：

- 将第$i$行中的所有参赛者向西移动$k$个方格。换句话说，在$(i,p)$中的选手被移动到$(i,p-k)$。
- 将第$i$行中的所有参赛者向东移动$k$个方格。换句话说，在$(i,p)$中的选手被移动到$(i,p+k)$。

每次操作后，$Z$的值将变为$Z~\text{OR}~k$，其中$\text{OR}$是按位或运算。请注意，PC可以多次对同一行执行操作。还要注意，PC不允许将参赛者移出网格。

有$Q$个问题。对于第$j$个问题，您将得到一个正整数$W_j$，PC必须执行零或更多操作，以便$Z$的最终值正好是$W_j$。将$M$定义为最大的数字，以便在所有操作之后，至少有一列正好包含$M$参赛者。对于每个问题，您必须找到PC可以完成的所有操作序列的最大可能$M$。请注意，PC针对一个问题所做的操作不会延续到其他问题。

**输入输出数据格式：**

**输入格式：**

第一行包含一个整数$N(1\leq N\leq 10^5)$，即网格中的行数以及参与OSN 2019的省份数。

接下来$N$行的第$i$行包含两个整数$L_i$和$R_i(1\leq L_i\leq R_i\leq 10^9)$，描述代表省$i$的参赛者的位置。

下一行包含将询问的问题数$Q(1\leq Q\leq 10^5)$。

接下来$Q$行的第$j$行包含一个整数$W_j(1\leq W_j\leq 10^9)$即第$j$个问题所需的最终值$Z$。

**输出格式：**

输出$Q$行，第$j$行包含一个整数，即第$j$个问题中$M$的最大值。**题目大意：** PC正在前往马纳多。原来，2019年印度尼西亚国家科学奥林匹克运动会正在举行。OSN 2019的参赛者目前正在一个待拍照的场地排队。该场地的形状类似于一个大小为$N\times 10^{100}$的网格，有$N$行和$10^{100}$列。行从北到南从$1$编号到$N$，列从西到东从$1$编号到$10^{100}$。第$r$行第$c$列的方格坐标为$(r,c)$。 有$N$个省份参加OSN 2019。最初，代表省$i$的每个参赛者都会站在方格$(i,p)$中，并满足$L_i\leq p\leq R_i$。因此，我们可以看到有$R_i-L_i+1$个参赛者代表省$i$。 PC的变量$Z$最初等于$0$。在一次操作中，PC可以选择行$i$和正整数$k$。然后，PC将执行以下两种操作之一： - 将第$i$行中的所有参赛者向西移动$k$个方格。换句话说，在$(i,p)$中的选手被移动到$(i,p-k)$。 - 将第$i$行中的所有参赛者向东移动$k$个方格。换句话说，在$(i,p)$中的选手被移动到$(i,p+k)$。 每次操作后，$Z$的值将变为$Z~\text{OR}~k$，其中$\text{OR}$是按位或运算。请注意，PC可以多次对同一行执行操作。还要注意，PC不允许将参赛者移出网格。 有$Q$个问题。对于第$j$个问题，您将得到一个正整数$W_j$，PC必须执行零或更多操作，以便$Z$的最终值正好是$W_j$。将$M$定义为最大的数字，以便在所有操作之后，至少有一列正好包含$M$参赛者。对于每个问题，您必须找到PC可以完成的所有操作序列的最大可能$M$。请注意，PC针对一个问题所做的操作不会延续到其他问题。 **输入输出数据格式：** **输入格式：** 第一行包含一个整数$N(1\leq N\leq 10^5)$，即网格中的行数以及参与OSN 2019的省份数。 接下来$N$行的第$i$行包含两个整数$L_i$和$R_i(1\leq L_i\leq R_i\leq 10^9)$，描述代表省$i$的参赛者的位置。 下一行包含将询问的问题数$Q(1\leq Q\leq 10^5)$。 接下来$Q$行的第$j$行包含一个整数$W_j(1\leq W_j\leq 10^9)$即第$j$个问题所需的最终值$Z$。 **输出格式：** 输出$Q$行，第$j$行包含一个整数，即第$j$个问题中$M$的最大值。