309718: CF1725C. Circular Mirror
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Circular Mirror
题意翻译
一个圆上有 $N$ 个可染色的点,编号 $1\to N$。$N$ 号点和 $1$ 号点相邻。 你可以用 $M$ 种颜色将这些点染色。要求不能出现有三个同色点围成直角三角形。 请求出全部合法方案的总数,输出它模 $998\ 244\ 353$ 的值。题目描述
Pak Chanek has a mirror in the shape of a circle. There are $ N $ lamps on the circumference numbered from $ 1 $ to $ N $ in clockwise order. The length of the arc from lamp $ i $ to lamp $ i+1 $ is $ D_i $ for $ 1 \leq i \leq N-1 $ . Meanwhile, the length of the arc between lamp $ N $ and lamp $ 1 $ is $ D_N $ . Pak Chanek wants to colour the lamps with $ M $ different colours. Each lamp can be coloured with one of the $ M $ colours. However, there cannot be three different lamps such that the colours of the three lamps are the same and the triangle made by considering the three lamps as vertices is a right triangle (triangle with one of its angles being exactly $ 90 $ degrees). The following are examples of lamp colouring configurations on the circular mirror. 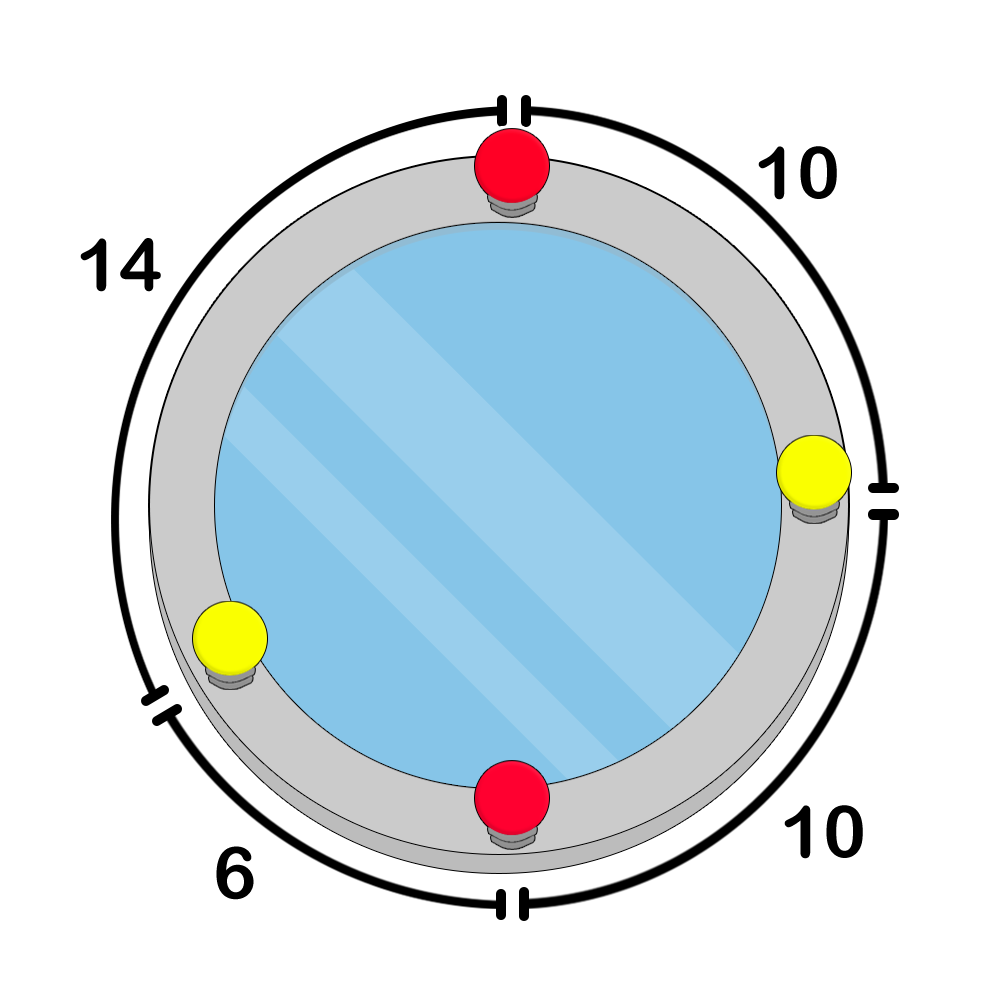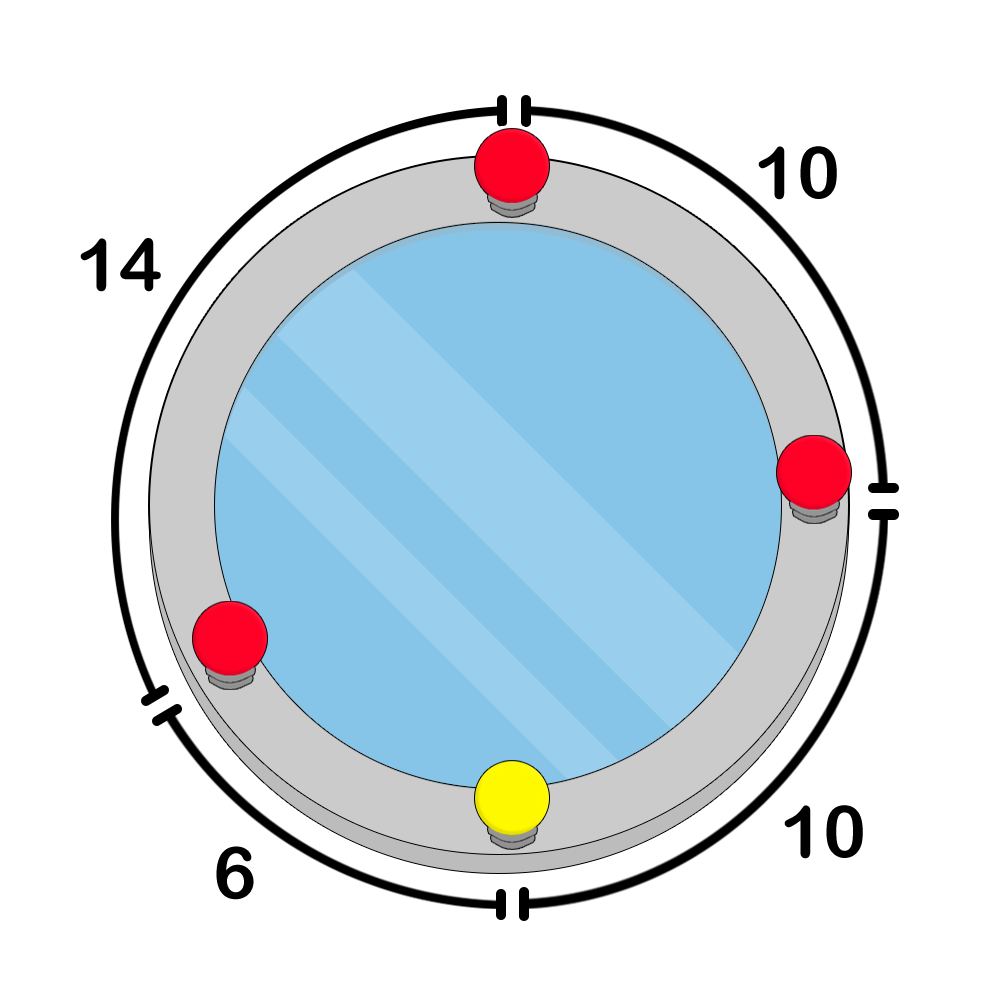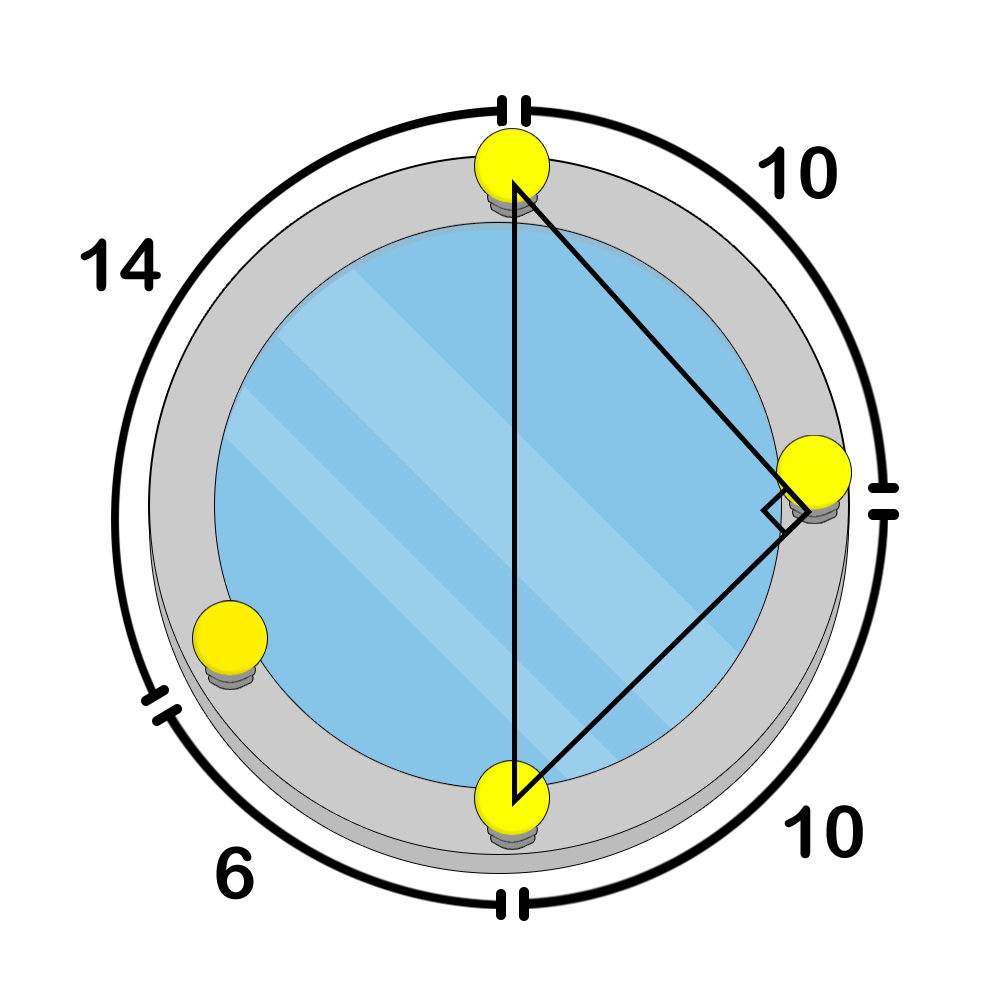Figure 1. an example of an incorrect colouring because lamps $ 1 $ , $ 2 $ , and $ 3 $ form a right triangleFigure 2. an example of a correct colouringFigure 3. an example of a correct colouringBefore colouring the lamps, Pak Chanek wants to know the number of distinct colouring configurations he can make. Count the number of distinct possible lamp colouring configurations, modulo $ 998\,244\,353 $ .输入输出格式
输入格式
The first line contains two integers $ N $ and $ M $ ( $ 1 \le N \le 3 \cdot 10^5 $ , $ 2 \le M \le 3 \cdot 10^5 $ ) — the number of lamps in the mirror and the number of different colours used. The second line contains $ N $ integers $ D_1, D_2, \ldots, D_N $ ( $ 1 \le D_i \le 10^9 $ ) — the lengths of the arcs between the lamps in the mirror.
输出格式
An integer representing the number of possible lamp colouring configurations, modulo $ 998\,244\,353 $ .
输入输出样例
输入样例 #1
4 2
10 10 6 14输出样例 #1
10输入样例 #2
1 2
10输出样例 #2
2说明
In the first example, all correct lamp colouring configurations are $ [1, 1, 2, 1] $ , $ [1, 1, 2, 2] $ , $ [1, 2, 1, 2] $ , $ [1, 2, 2, 1] $ , $ [1, 2, 2, 2] $ , $ [2, 1, 1, 1] $ , $ [2, 1, 1, 2] $ , $ [2, 1, 2, 1] $ , $ [2, 2, 1, 1] $ , and $ [2, 2, 1, 2] $ .Input
题意翻译
一个圆上有 $N$ 个可染色的点,编号 $1\to N$。$N$ 号点和 $1$ 号点相邻。 你可以用 $M$ 种颜色将这些点染色。要求不能出现有三个同色点围成直角三角形。 请求出全部合法方案的总数,输出它模 $998\ 244\ 353$ 的值。Output
**圆形镜子**
**题意翻译:**
一个圆周上有N个可染色的点,编号为1到N,其中N号点和1号点相邻。可以使用M种颜色对这些点进行染色,但不能出现三个同色点围成一个直角三角形。求出所有合法的染色方案总数,并输出其除以998,244,353的余数。
**题目描述:**
Pak Chanek有一个圆形的镜子,圆周上有N盏灯,编号从1到N,顺时针排列。灯i到灯i+1之间的圆弧长度为$ D_i $(对于1≤i≤N-1),同时灯N到灯1之间的圆弧长度为$ D_N $。
Pak Chanek想要用M种不同的颜色来染色这些灯。每盏灯可以用M种颜色中的一种进行染色。然而,不能有三个不同的灯,它们颜色相同,并且这三个灯作为顶点构成的三角形是一个直角三角形(其中一个角恰好为90度)。
在染色之前,Pak Chanek想要知道他可以制作的不同染色配置的数量。计算不同的灯染色配置的数量,模数为998,244,353。
**输入输出格式:**
**输入格式:**
第一行包含两个整数N和M(1≤N≤3×10^5,2≤M≤3×10^5)——镜中灯的数量和使用的不同颜色的数量。
第二行包含N个整数$ D_1, D_2, \ldots, D_N $(1≤$ D_i $≤10^9)——镜中灯之间的圆弧长度。
**输出格式:**
一个整数,表示可能的灯染色配置的数量,模数为998,244,353。
**输入输出样例:**
**输入样例 #1:**
```
4 2
10 10 6 14
```
**输出样例 #1:**
```
10
```
**输入样例 #2:**
```
1 2
10
```
**输出样例 #2:**
```
2
```
**说明:**
在第一个例子中,所有正确的灯染色配置如下:
```
[1, 1, 2, 1], [1, 1, 2, 2], [1, 2, 1, 2], [1, 2, 2, 1],
[1, 2, 2, 2], [2, 1, 1, 1], [2, 1, 1, 2], [2, 1, 2, 1],
[2, 2, 1, 1], [2, 2, 1, 2]
```**圆形镜子** **题意翻译:** 一个圆周上有N个可染色的点,编号为1到N,其中N号点和1号点相邻。可以使用M种颜色对这些点进行染色,但不能出现三个同色点围成一个直角三角形。求出所有合法的染色方案总数,并输出其除以998,244,353的余数。 **题目描述:** Pak Chanek有一个圆形的镜子,圆周上有N盏灯,编号从1到N,顺时针排列。灯i到灯i+1之间的圆弧长度为$ D_i $(对于1≤i≤N-1),同时灯N到灯1之间的圆弧长度为$ D_N $。 Pak Chanek想要用M种不同的颜色来染色这些灯。每盏灯可以用M种颜色中的一种进行染色。然而,不能有三个不同的灯,它们颜色相同,并且这三个灯作为顶点构成的三角形是一个直角三角形(其中一个角恰好为90度)。 在染色之前,Pak Chanek想要知道他可以制作的不同染色配置的数量。计算不同的灯染色配置的数量,模数为998,244,353。 **输入输出格式:** **输入格式:** 第一行包含两个整数N和M(1≤N≤3×10^5,2≤M≤3×10^5)——镜中灯的数量和使用的不同颜色的数量。 第二行包含N个整数$ D_1, D_2, \ldots, D_N $(1≤$ D_i $≤10^9)——镜中灯之间的圆弧长度。 **输出格式:** 一个整数,表示可能的灯染色配置的数量,模数为998,244,353。 **输入输出样例:** **输入样例 #1:** ``` 4 2 10 10 6 14 ``` **输出样例 #1:** ``` 10 ``` **输入样例 #2:** ``` 1 2 10 ``` **输出样例 #2:** ``` 2 ``` **说明:** 在第一个例子中,所有正确的灯染色配置如下: ``` [1, 1, 2, 1], [1, 1, 2, 2], [1, 2, 1, 2], [1, 2, 2, 1], [1, 2, 2, 2], [2, 1, 1, 1], [2, 1, 1, 2], [2, 1, 2, 1], [2, 2, 1, 1], [2, 2, 1, 2] ```
**题意翻译:**
一个圆周上有N个可染色的点,编号为1到N,其中N号点和1号点相邻。可以使用M种颜色对这些点进行染色,但不能出现三个同色点围成一个直角三角形。求出所有合法的染色方案总数,并输出其除以998,244,353的余数。
**题目描述:**
Pak Chanek有一个圆形的镜子,圆周上有N盏灯,编号从1到N,顺时针排列。灯i到灯i+1之间的圆弧长度为$ D_i $(对于1≤i≤N-1),同时灯N到灯1之间的圆弧长度为$ D_N $。
Pak Chanek想要用M种不同的颜色来染色这些灯。每盏灯可以用M种颜色中的一种进行染色。然而,不能有三个不同的灯,它们颜色相同,并且这三个灯作为顶点构成的三角形是一个直角三角形(其中一个角恰好为90度)。
在染色之前,Pak Chanek想要知道他可以制作的不同染色配置的数量。计算不同的灯染色配置的数量,模数为998,244,353。
**输入输出格式:**
**输入格式:**
第一行包含两个整数N和M(1≤N≤3×10^5,2≤M≤3×10^5)——镜中灯的数量和使用的不同颜色的数量。
第二行包含N个整数$ D_1, D_2, \ldots, D_N $(1≤$ D_i $≤10^9)——镜中灯之间的圆弧长度。
**输出格式:**
一个整数,表示可能的灯染色配置的数量,模数为998,244,353。
**输入输出样例:**
**输入样例 #1:**
```
4 2
10 10 6 14
```
**输出样例 #1:**
```
10
```
**输入样例 #2:**
```
1 2
10
```
**输出样例 #2:**
```
2
```
**说明:**
在第一个例子中,所有正确的灯染色配置如下:
```
[1, 1, 2, 1], [1, 1, 2, 2], [1, 2, 1, 2], [1, 2, 2, 1],
[1, 2, 2, 2], [2, 1, 1, 1], [2, 1, 1, 2], [2, 1, 2, 1],
[2, 2, 1, 1], [2, 2, 1, 2]
```**圆形镜子** **题意翻译:** 一个圆周上有N个可染色的点,编号为1到N,其中N号点和1号点相邻。可以使用M种颜色对这些点进行染色,但不能出现三个同色点围成一个直角三角形。求出所有合法的染色方案总数,并输出其除以998,244,353的余数。 **题目描述:** Pak Chanek有一个圆形的镜子,圆周上有N盏灯,编号从1到N,顺时针排列。灯i到灯i+1之间的圆弧长度为$ D_i $(对于1≤i≤N-1),同时灯N到灯1之间的圆弧长度为$ D_N $。 Pak Chanek想要用M种不同的颜色来染色这些灯。每盏灯可以用M种颜色中的一种进行染色。然而,不能有三个不同的灯,它们颜色相同,并且这三个灯作为顶点构成的三角形是一个直角三角形(其中一个角恰好为90度)。 在染色之前,Pak Chanek想要知道他可以制作的不同染色配置的数量。计算不同的灯染色配置的数量,模数为998,244,353。 **输入输出格式:** **输入格式:** 第一行包含两个整数N和M(1≤N≤3×10^5,2≤M≤3×10^5)——镜中灯的数量和使用的不同颜色的数量。 第二行包含N个整数$ D_1, D_2, \ldots, D_N $(1≤$ D_i $≤10^9)——镜中灯之间的圆弧长度。 **输出格式:** 一个整数,表示可能的灯染色配置的数量,模数为998,244,353。 **输入输出样例:** **输入样例 #1:** ``` 4 2 10 10 6 14 ``` **输出样例 #1:** ``` 10 ``` **输入样例 #2:** ``` 1 2 10 ``` **输出样例 #2:** ``` 2 ``` **说明:** 在第一个例子中,所有正确的灯染色配置如下: ``` [1, 1, 2, 1], [1, 1, 2, 2], [1, 2, 1, 2], [1, 2, 2, 1], [1, 2, 2, 2], [2, 1, 1, 1], [2, 1, 1, 2], [2, 1, 2, 1], [2, 2, 1, 1], [2, 2, 1, 2] ```