Path Prefixes

题意翻译

# Path Prefixes ## 题目描述 现有一颗以 $1$ 为根的树，节点编号从 $1$ 到 $n$ . 每条边有两个权值，分别为 $a_j$ 和 $b_j$ . 输出 $n-1$ 个数 $r_2,r_3 \cdots ,r_n$ ，其中 $r_i$ 定义如下: 考虑从根节点( $1$ 号节点 ) 到第 $i$ 号节点 $(2 \le i \le n)$ 的路径，令沿该路径 $a_j$ 的花费为 $A_i$ ， $r_i$ 为该路径的最长前缀，使该前缀的 $b_j$ 之和不大于 $A_i$ . 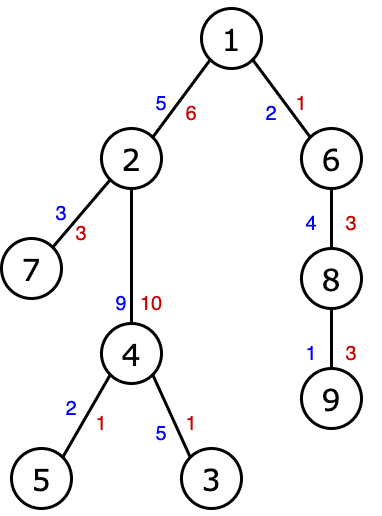 以 $n=9$ 时为例，如上图，蓝色数字表示 $a_j$ 的花费，红色数字表示 $b_j$ 的花费. 在这种情况下： - $ r_2=0 $ ， 因为到节点 $ 2 $ 的路径中有 $ a_j=5 $ ， 只有前缀为 $ 0 $ 时才可能有较小（或相等）的 $ b_j $ ； - $ r_3=3 $ ， 因为到节点 $ 3 $ 的路径中 $ a_j $ 为 $ 5+9+5=19 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 6+10+1=17 $ ( $ 17 \le 19 $ 符合题意 )； - $ r_4=1 $ ， 因为到节点 $ 4 $ 的路径中 $ a_j $ 为 $ 5+9=14 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 为 $ 6 $ (这是最长的符合题意的前缀， 因为长为 $ 2 $ 的前缀的 $ b_j $ 为 $ 6+10=16 $ ， 大于 $ 14 $ )； - $ r_5=2 $ ， 因为到节点 $ 5 $ 的路径中 $ a_j $ 为 $ 5+9+2=16 $ ， 长为 $ 2 $ 的前缀使 $ b_j $ 为 $ 6+10=16 $ (这是最长的符合题意的前缀， 因为长为 $ 3 $ 的前缀的 $ b_j $ 为 $ 6+10+1=17 $ ， 比 $ 16 $ 大 )； - $ r_6=1 $ ， 因为到节点 $ 6 $ 的路径中 $ a_j $ 为 $ 2 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 1 $ ； - $ r_7=1 $ ， 因为到节点 $ 7 $ 的路径中 $ a_j $ 为 $ 5+3=8 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 6 $ (这是最长的符合题意的前缀， 因为长为 $ 2 $ 的前缀的 $ b_j $ 为 $ 6+3=9 $ ， 超出了期望的 $ 8 $ )； - $ r_8=2 $ ， 因为到节点 $ 8 $ 的路径中 $ a_j $ 为 $ 2+4=6 $ ， 长为 $ 2 $ 的前缀使 $ b_j $ 为 $ 1+3=4 $ ； - $ r_9=3 $ ， 因为到节点 $ 9 $ 的路径中 $ a_j $ 为 $ 2+4+1=7 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 1+3+3=7 $ . ## 输入格式 第一行有一个整数 $ t $ ( $ 1 \le t \le 10^4 $ ) 表示测试组数. 每组样例以一个整数 $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ) 开始，表示这棵树的节点数. 接下来 $ n-1 $ 行，每行有三个整数 $ p_j， a_j， b_j $ ( $ 1 \le p_j \le n $ ; $ 1 \le a_j,b_j \le 10^9 $ ) 分别表示节点 $ j $ 的祖先和从 $ p_j $ 到 $ j $ 的两个边权. $ j $ 的值从 $ 2 $ 到 $ n $ . 输入数据保证生成的是一颗以 $ 1 $ 根的树，且 $ n $ 不超过 $ 2\cdot10^5 $ . ## 输出格式 对于每一组输入，输出一行 $ n-1 $ 个数: $ r_2, r_3, \dots , r_n $ . ## 样例 #1 ### 样例输入 #1 ``` 4 9 1 5 6 4 5 1 2 9 10 4 2 1 1 2 1 2 3 3 6 4 3 8 1 3 4 1 1 100 2 1 1 3 101 1 4 1 100 1 2 1 1 3 1 101 10 1 1 4 2 3 5 2 5 1 3 4 3 3 1 5 5 3 5 5 2 1 1 3 2 6 2 1 ``` ### 样例输出 #1 ``` 0 3 1 2 1 1 2 3 0 0 3 1 2 2 0 1 2 1 1 2 2 1 1 ``` ## 提示 第一组样例的解释包含在题目描述中 在第二组样例中 - $ r_2=0 $ ，因为到节点 $ 2 $ 的路径中 $ a_j $ 等于 $ 1 $ ， 只有前缀为 $ 0 $ 时才可能有较小（或相等）的 $ b_j $ - $ r_3=0 $ ， 因为到节点 $ 3 $ 的路径中 $ a_j $ 为 $ 1+1=2 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 100 $ ( $ 100 > 2 $ )； - $ r_4=3 $ ， 因为到节点 $ 4 $ 的路径中 of $ a_j $ 为 $ 1+1+101=103 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 102 $ .

题目描述

You are given a rooted tree. It contains $ n $ vertices, which are numbered from $ 1 $ to $ n $ . The root is the vertex $ 1 $ . Each edge has two positive integer values. Thus, two positive integers $ a_j $ and $ b_j $ are given for each edge. Output $ n-1 $ numbers $ r_2, r_3, \dots, r_n $ , where $ r_i $ is defined as follows. Consider the path from the root (vertex $ 1 $ ) to $ i $ ( $ 2 \le i \le n $ ). Let the sum of the costs of $ a_j $ along this path be $ A_i $ . Then $ r_i $ is equal to the length of the maximum prefix of this path such that the sum of $ b_j $ along this prefix does not exceed $ A_i $ . Example for $ n=9 $ . The blue color shows the costs of $ a_j $ , and the red color shows the costs of $ b_j $ .Consider an example. In this case: - $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 5 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ; - $ r_3=3 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 5+9+5=19 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 6+10+1=17 $ ( the number is $ 17 \le 19 $ ); - $ r_4=1 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 5+9=14 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+10=16 $ , which is more than $ 14 $ ); - $ r_5=2 $ , since the path to $ 5 $ has an amount of $ a_j $ equal to $ 5+9+2=16 $ , the prefix of length $ 2 $ of this path has a sum of $ b_j $ equal to $ 6+10=16 $ (this is the longest suitable prefix, since the prefix of length $ 3 $ already has an amount of $ b_j $ equal to $ 6+10+1=17 $ , what is more than $ 16 $ ); - $ r_6=1 $ , since the path up to $ 6 $ has an amount of $ a_j $ equal to $ 2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 1 $ ; - $ r_7=1 $ , since the path to $ 7 $ has an amount of $ a_j $ equal to $ 5+3=8 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+3=9 $ , which is more than $ 8 $ ); - $ r_8=2 $ , since the path up to $ 8 $ has an amount of $ a_j $ equal to $ 2+4=6 $ , the prefix of length $ 2 $ of this path has an amount of $ b_j $ equal to $ 1+3=4 $ ; - $ r_9=3 $ , since the path to $ 9 $ has an amount of $ a_j $ equal to $ 2+4+1=7 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 1+3+3=7 $ .

输入输出格式

输入格式

The first line contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test. The descriptions of test cases follow. Each description begins with a line that contains an integer $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ) — the number of vertices in the tree. This is followed by $ n-1 $ string, each of which contains three numbers $ p_j, a_j, b_j $ ( $ 1 \le p_j \le n $ ; $ 1 \le a_j,b_j \le 10^9 $ ) — the ancestor of the vertex $ j $ , the first and second values an edge that leads from $ p_j $ to $ j $ . The value of $ j $ runs through all values from $ 2 $ to $ n $ inclusive. It is guaranteed that each set of input data has a correct hanged tree with a root at the vertex $ 1 $ . It is guaranteed that the sum of $ n $ over all input test cases does not exceed $ 2\cdot10^5 $ .

输出格式

For each test case, output $ n-1 $ integer in one line: $ r_2, r_3, \dots, r_n $ .

输入输出样例

输入样例 #1

4
9
1 5 6
4 5 1
2 9 10
4 2 1
1 2 1
2 3 3
6 4 3
8 1 3
4
1 1 100
2 1 1
3 101 1
4
1 100 1
2 1 1
3 1 101
10
1 1 4
2 3 5
2 5 1
3 4 3
3 1 5
5 3 5
5 2 1
1 3 2
6 2 1

输出样例 #1

0 3 1 2 1 1 2 3 
0 0 3 
1 2 2 
0 1 2 1 1 2 2 1 1

说明

The first example is clarified in the statement. In the second example: - $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 1 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ; - $ r_3=0 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 1+1=2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 100 $ ( $ 100 > 2 $ ); - $ r_4=3 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 1+1+101=103 $ , the prefix of length $ 3 $ of this path has an amount of $ b_j $ equal to $ 102 $ , .

题意翻译

# Path Prefixes ## 题目描述 现有一颗以 $1$ 为根的树，节点编号从 $1$ 到 $n$ . 每条边有两个权值，分别为 $a_j$ 和 $b_j$ . 输出 $n-1$ 个数 $r_2,r_3 \cdots ,r_n$ ，其中 $r_i$ 定义如下: 考虑从根节点( $1$ 号节点 ) 到第 $i$ 号节点 $(2 \le i \le n)$ 的路径，令沿该路径 $a_j$ 的花费为 $A_i$ ， $r_i$ 为该路径的最长前缀，使该前缀的 $b_j$ 之和不大于 $A_i$ .  以 $n=9$ 时为例，如上图，蓝色数字表示 $a_j$ 的花费，红色数字表示 $b_j$ 的花费. 在这种情况下： - $ r_2=0 $ ， 因为到节点 $ 2 $ 的路径中有 $ a_j=5 $ ， 只有前缀为 $ 0 $ 时才可能有较小（或相等）的 $ b_j $ ； - $ r_3=3 $ ， 因为到节点 $ 3 $ 的路径中 $ a_j $ 为 $ 5+9+5=19 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 6+10+1=17 $ ( $ 17 \le 19 $ 符合题意 )； - $ r_4=1 $ ， 因为到节点 $ 4 $ 的路径中 $ a_j $ 为 $ 5+9=14 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 为 $ 6 $ (这是最长的符合题意的前缀， 因为长为 $ 2 $ 的前缀的 $ b_j $ 为 $ 6+10=16 $ ， 大于 $ 14 $ )； - $ r_5=2 $ ， 因为到节点 $ 5 $ 的路径中 $ a_j $ 为 $ 5+9+2=16 $ ， 长为 $ 2 $ 的前缀使 $ b_j $ 为 $ 6+10=16 $ (这是最长的符合题意的前缀， 因为长为 $ 3 $ 的前缀的 $ b_j $ 为 $ 6+10+1=17 $ ， 比 $ 16 $ 大 )； - $ r_6=1 $ ， 因为到节点 $ 6 $ 的路径中 $ a_j $ 为 $ 2 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 1 $ ； - $ r_7=1 $ ， 因为到节点 $ 7 $ 的路径中 $ a_j $ 为 $ 5+3=8 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 6 $ (这是最长的符合题意的前缀， 因为长为 $ 2 $ 的前缀的 $ b_j $ 为 $ 6+3=9 $ ， 超出了期望的 $ 8 $ )； - $ r_8=2 $ ， 因为到节点 $ 8 $ 的路径中 $ a_j $ 为 $ 2+4=6 $ ， 长为 $ 2 $ 的前缀使 $ b_j $ 为 $ 1+3=4 $ ； - $ r_9=3 $ ， 因为到节点 $ 9 $ 的路径中 $ a_j $ 为 $ 2+4+1=7 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 1+3+3=7 $ . ## 输入格式 第一行有一个整数 $ t $ ( $ 1 \le t \le 10^4 $ ) 表示测试组数. 每组样例以一个整数 $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ) 开始，表示这棵树的节点数. 接下来 $ n-1 $ 行，每行有三个整数 $ p_j， a_j， b_j $ ( $ 1 \le p_j \le n $ ; $ 1 \le a_j,b_j \le 10^9 $ ) 分别表示节点 $ j $ 的祖先和从 $ p_j $ 到 $ j $ 的两个边权. $ j $ 的值从 $ 2 $ 到 $ n $ . 输入数据保证生成的是一颗以 $ 1 $ 根的树，且 $ n $ 不超过 $ 2\cdot10^5 $ . ## 输出格式 对于每一组输入，输出一行 $ n-1 $ 个数: $ r_2, r_3, \dots , r_n $ . ## 样例 #1 ### 样例输入 #1 ``` 4 9 1 5 6 4 5 1 2 9 10 4 2 1 1 2 1 2 3 3 6 4 3 8 1 3 4 1 1 100 2 1 1 3 101 1 4 1 100 1 2 1 1 3 1 101 10 1 1 4 2 3 5 2 5 1 3 4 3 3 1 5 5 3 5 5 2 1 1 3 2 6 2 1 ``` ### 样例输出 #1 ``` 0 3 1 2 1 1 2 3 0 0 3 1 2 2 0 1 2 1 1 2 2 1 1 ``` ## 提示 第一组样例的解释包含在题目描述中 在第二组样例中 - $ r_2=0 $ ，因为到节点 $ 2 $ 的路径中 $ a_j $ 等于 $ 1 $ ， 只有前缀为 $ 0 $ 时才可能有较小（或相等）的 $ b_j $ - $ r_3=0 $ ， 因为到节点 $ 3 $ 的路径中 $ a_j $ 为 $ 1+1=2 $ ， 长为 $ 1 $ 的前缀使 $ b_j $ 等于 $ 100 $ ( $ 100 > 2 $ )； - $ r_4=3 $ ， 因为到节点 $ 4 $ 的路径中 of $ a_j $ 为 $ 1+1+101=103 $ ， 长为 $ 3 $ 的前缀使 $ b_j $ 为 $ 102 $ .