Making Towers

题意翻译

给定一个长为 $n$ 的颜色序列 $\{c_n\}$。你初始位于坐标 $(0,0)$。假设你当前位于坐标 $(x,y)$，每次移动，你可以走到 $(x,y+1)$，$(x+1,y)$，$(x-1,y)$（即往上、左、右走一格）。第 $i$ 次移动前的格子将会被染上颜色 $c_i$。 对于每种颜色 $r$，求解：最大的整数 $s$，使得存在一种移动方案，存在坐标 $(x,y)$，且 $\forall i\in[1,s]$，$(x,y+i-1)$ 的颜色为 $r$（即，有一个 $1\times s$ 的颜色全为 $r$ 的横条）。 多测，$1\le t \le 10^4$，$1\le n\le 10^5$，$1\le c_i\le n$，$\sum n\le 2\times 10^5$。 Translated by @Sya_Resory

题目描述

You have a sequence of $ n $ colored blocks. The color of the $ i $ -th block is $ c_i $ , an integer between $ 1 $ and $ n $ . You will place the blocks down in sequence on an infinite coordinate grid in the following way. 1. Initially, you place block $ 1 $ at $ (0, 0) $ . 2. For $ 2 \le i \le n $ , if the $ (i - 1) $ -th block is placed at position $ (x, y) $ , then the $ i $ -th block can be placed at one of positions $ (x + 1, y) $ , $ (x - 1, y) $ , $ (x, y + 1) $ (but not at position $ (x, y - 1) $ ), as long no previous block was placed at that position. A tower is formed by $ s $ blocks such that they are placed at positions $ (x, y), (x, y + 1), \ldots, (x, y + s - 1) $ for some position $ (x, y) $ and integer $ s $ . The size of the tower is $ s $ , the number of blocks in it. A tower of color $ r $ is a tower such that all blocks in it have the color $ r $ . For each color $ r $ from $ 1 $ to $ n $ , solve the following problem independently: - Find the maximum size of a tower of color $ r $ that you can form by placing down the blocks according to the rules.

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ). The second line of each test case contains $ n $ integers $ c_1, c_2, \ldots, c_n $ ( $ 1 \le c_i \le n $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, output $ n $ integers. The $ r $ -th of them should be the maximum size of an tower of color $ r $ you can form by following the given rules. If you cannot form any tower of color $ r $ , the $ r $ -th integer should be $ 0 $ .

输入输出样例

输入样例 #1

6
7
1 2 3 1 2 3 1
6
4 2 2 2 4 4
1
1
5
5 4 5 3 5
6
3 3 3 1 3 3
8
1 2 3 4 4 3 2 1

输出样例 #1

3 2 2 0 0 0 0 
0 3 0 2 0 0 
1 
0 0 1 1 1 
1 0 4 0 0 0 
2 2 2 2 0 0 0 0

说明

In the first test case, one of the possible ways to form a tower of color $ 1 $ and size $ 3 $ is: - place block $ 1 $ at position $ (0, 0) $ ; - place block $ 2 $ to the right of block $ 1 $ , at position $ (1, 0) $ ; - place block $ 3 $ above block $ 2 $ , at position $ (1, 1) $ ; - place block $ 4 $ to the left of block $ 3 $ , at position $ (0, 1) $ ; - place block $ 5 $ to the left of block $ 4 $ , at position $ (-1, 1) $ ; - place block $ 6 $ above block $ 5 $ , at position $ (-1, 2) $ ; - place block $ 7 $ to the right of block $ 6 $ , at position $ (0, 2) $ . 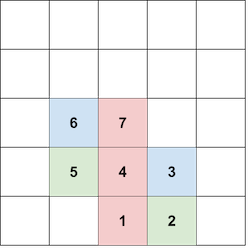The blocks at positions $ (0, 0) $ , $ (0, 1) $ , and $ (0, 2) $ all have color $ 1 $ , forming an tower of size $ 3 $ . In the second test case, note that the following placement is not valid, since you are not allowed to place block $ 6 $ under block $ 5 $ : 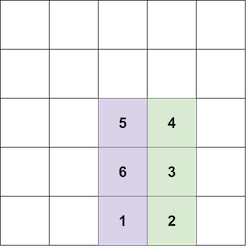It can be shown that it is impossible to form a tower of color $ 4 $ and size $ 3 $ .

**题目大意：**
有一个长度为 $ n $ 的颜色序列 $\{c_n\}$。你从坐标 $(0,0)$ 开始，每次可以向上、左、右走一格。在每次移动前，你的位置会被染上序列中对应的颜色。对于每种颜色 $ r $，你需要找到最大的整数 $ s $，使得存在一种移动方案，在某个坐标 $(x,y)$ 上方，形成一个 $ 1 \times s $ 的全为颜色 $ r $ 的横条。

**输入输出数据格式：**
- **输入格式：**
- 第一行包含一个整数 $ t $（$ 1 \le t \le 10^4 $），表示测试用例的数量。
- 每个测试用例第一行包含一个整数 $ n $（$ 1 \le n \le 10^5 $）。
- 每个测试用例的第二行包含 $ n $ 个整数 $ c_1, c_2, \ldots, c_n $（$ 1 \le c_i \le n $）。
- 保证所有测试用例的 $ n $ 之和不超过 $ 2 \times 10^5 $。
- **输出格式：**
- 对于每个测试用例，输出 $ n $ 个整数。第 $ r $ 个整数表示按照给定规则，你能形成的颜色 $ r $ 的塔的最大大小。如果你不能形成任何颜色 $ r $ 的塔，则第 $ r $ 个整数为 $ 0 $。

**输入输出样例：**
- **输入样例 #1：**
```
6
7
1 2 3 1 2 3 1
6
4 2 2 2 4 4
1
1
5
5 4 5 3 5
6
3 3 3 1 3 3
8
1 2 3 4 4 3 2 1
```
- **输出样例 #1：**
```
3 2 2 0 0 0 0
0 3 0 2 0 0
1
0 0 1 1 1
1 0 4 0 0 0
2 2 2 2 0 0 0 0
```**题目大意：** 有一个长度为 $ n $ 的颜色序列 $\{c_n\}$。你从坐标 $(0,0)$ 开始，每次可以向上、左、右走一格。在每次移动前，你的位置会被染上序列中对应的颜色。对于每种颜色 $ r $，你需要找到最大的整数 $ s $，使得存在一种移动方案，在某个坐标 $(x,y)$ 上方，形成一个 $ 1 \times s $ 的全为颜色 $ r $ 的横条。 **输入输出数据格式：** - **输入格式：** - 第一行包含一个整数 $ t $（$ 1 \le t \le 10^4 $），表示测试用例的数量。 - 每个测试用例第一行包含一个整数 $ n $（$ 1 \le n \le 10^5 $）。 - 每个测试用例的第二行包含 $ n $ 个整数 $ c_1, c_2, \ldots, c_n $（$ 1 \le c_i \le n $）。 - 保证所有测试用例的 $ n $ 之和不超过 $ 2 \times 10^5 $。 - **输出格式：** - 对于每个测试用例，输出 $ n $ 个整数。第 $ r $ 个整数表示按照给定规则，你能形成的颜色 $ r $ 的塔的最大大小。如果你不能形成任何颜色 $ r $ 的塔，则第 $ r $ 个整数为 $ 0 $。 **输入输出样例：** - **输入样例 #1：** ``` 6 7 1 2 3 1 2 3 1 6 4 2 2 2 4 4 1 1 5 5 4 5 3 5 6 3 3 3 1 3 3 8 1 2 3 4 4 3 2 1 ``` - **输出样例 #1：** ``` 3 2 2 0 0 0 0 0 3 0 2 0 0 1 0 0 1 1 1 1 0 4 0 0 0 2 2 2 2 0 0 0 0 ```