Optimal Path

题意翻译

# 最优路径 ## 题目描述 你得到一个大小为 $ n \times m $ 的表 $ a $ 。我们将考虑从上到下从 $1$ 到 $n$ 编号的表格行，从左到右从 $1$ 到 $m$ 编号的列。我们将在 $ i $ -th 行和 $ j $ -th 列中的单元格表示为 $ (i, j) $ 。在单元格 $ (i, j) $ 中有一个数字 $ (i - 1) \cdot m + j $ ，即 $ a_{ij} = (i - 1) \cdot m + j $ 。 一只乌龟最初站在单元格 $ (1, 1) $ 中，它想来到单元格 $ (n, m) $ 。从单元格 $ (i, j) $ 它可以一步转到单元格 $ (i + 1, j) $ 或 $ (i, j + 1) $ 之一，如果它存在的话。路径是一系列单元格，其中对于序列中的每两个相邻单元格，满足以下条件：乌龟可以一步从第一个单元格到达第二个单元格。路径的成本是写入路径单元格中的数字的总和。 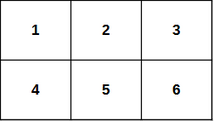例如，$ n = 2 $ 和 $ m = 3 $ 表格将如上所示。海龟可以走以下路径： $ (1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) $ 。这种方式的成本等于 $ a_{11} + a_{12} + a_{13} + a_{23} = 12 $ 。另一方面，路径 $ (1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1) $ 和 $ (1, 1) \rightarrow (1, 3) $是不正确的，因为在第一条路径中乌龟不能迈出一步 $ (2, 2) \rightarrow (2, 1) $ ，而在第二条路径中它不能迈出一步 $ (1, 1) \右箭头 (1, 3) $ 。 你被要求告诉海龟从单元 $ (1, 1) $ 到单元 $ (n, m) $ 的路径的最小可能成本。请注意，单元格 $ (1, 1) $ 和 $ (n, m) $ 是其中的一部分。 ## 输入格式 第一行包含一个整数 $ t $ ( $ 1 \leq t \leq 1000 $ ) — 测试用例的数量。测试用例的描述如下。 每个测试用例的一行包含两个整数 $ n $ 和 $ m $ ( $ 1 \leq n, m \leq 10^4 $ ) — 分别是表 $ a $ 的行数和列数。 ##输出格式 对于每个测试用例，输出一个整数——从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。 ## 样例#1 ### 样例输入示例 #1 ``` 7 1 1 2 3 3 2 7 1 1 10 5 5 10000 10000 ``` ### 样例输出#1 ``` 1 12 13 28 55 85 500099995000 ``` ## 提示 在第一个测试用例中，唯一可能的路径由单个单元格 $ (1, 1) $ 组成。 语句中显示了第二个测试用例中成本最低的路径。 在第四和第五个测试用例中，从 $ (1, 1) $ 到 $ (n, m) $ 只有一条路径。两条路径都访问表中的每个单元格。

题目描述

You are given a table $ a $ of size $ n \times m $ . We will consider the table rows numbered from top to bottom from $ 1 $ to $ n $ , and the columns numbered from left to right from $ 1 $ to $ m $ . We will denote a cell that is in the $ i $ -th row and in the $ j $ -th column as $ (i, j) $ . In the cell $ (i, j) $ there is written a number $ (i - 1) \cdot m + j $ , that is $ a_{ij} = (i - 1) \cdot m + j $ . A turtle initially stands in the cell $ (1, 1) $ and it wants to come to the cell $ (n, m) $ . From the cell $ (i, j) $ it can in one step go to one of the cells $ (i + 1, j) $ or $ (i, j + 1) $ , if it exists. A path is a sequence of cells in which for every two adjacent in the sequence cells the following satisfies: the turtle can reach from the first cell to the second cell in one step. A cost of a path is the sum of numbers that are written in the cells of the path. For example, with $ n = 2 $ and $ m = 3 $ the table will look as shown above. The turtle can take the following path: $ (1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) $ . The cost of such way is equal to $ a_{11} + a_{12} + a_{13} + a_{23} = 12 $ . On the other hand, the paths $ (1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1) $ and $ (1, 1) \rightarrow (1, 3) $ are incorrect, because in the first path the turtle can't make a step $ (2, 2) \rightarrow (2, 1) $ , and in the second path it can't make a step $ (1, 1) \rightarrow (1, 3) $ . You are asked to tell the turtle a minimal possible cost of a path from the cell $ (1, 1) $ to the cell $ (n, m) $ . Please note that the cells $ (1, 1) $ and $ (n, m) $ are a part of the way.

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases. The description of test cases follows. A single line of each test case contains two integers $ n $ and $ m $ ( $ 1 \leq n, m \leq 10^4 $ ) — the number of rows and columns of the table $ a $ respectively.

输出格式

For each test case output a single integer — a minimal possible cost of a path from the cell $ (1, 1) $ to the cell $ (n, m) $ .

输入输出样例

输入样例 #1

7
1 1
2 3
3 2
7 1
1 10
5 5
10000 10000

输出样例 #1

1
12
13
28
55
85
500099995000

说明

In the first test case the only possible path consists of a single cell $ (1, 1) $ . The path with the minimal cost in the second test case is shown in the statement. In the fourth and the fifth test cases there is only one path from $ (1, 1) $ to $ (n, m) $ . Both paths visit every cell in the table.

**最优路径**

## 题目描述
给定一个大小为 $ n \times m $ 的表 $ a $。表的行从上到下编号为 $ 1 $ 到 $ n $，列从左到右编号为 $ 1 $ 到 $ m $。单元格 $ (i, j) $ 中的数字为 $ (i - 1) \cdot m + j $，即 $ a_{ij} = (i - 1) \cdot m + j $。

一只乌龟最初位于单元格 $ (1, 1) $，它想要到达单元格 $ (n, m) $。从单元格 $ (i, j) $，它可以一步转移到单元格 $ (i + 1, j) $ 或 $ (i, j + 1) $（如果存在的话）。路径是单元格的序列，对于序列中的每两个相邻单元格，满足乌龟可以一步从第一个单元格到达第二个单元格的条件。路径的成本是路径单元格中数字的总和。

例如，当 $ n = 2 $ 和 $ m = 3 $ 时，表如下所示。乌龟可以走以下路径：$ (1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) $。这条路径的成本等于 $ a_{11} + a_{12} + a_{13} + a_{23} = 12 $。另一方面，路径 $ (1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1) $ 和 $ (1, 1) \rightarrow (1, 3) $ 是不正确的，因为在第一条路径中乌龟不能迈出一步 $ (2, 2) \rightarrow (2, 1) $，而在第二条路径中它不能迈出一步 $ (1, 1) \rightarrow (1, 3) $。

要求告诉乌龟从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。注意，单元格 $ (1, 1) $ 和 $ (n, m) $ 是路径的一部分。

## 输入格式
第一行包含一个整数 $ t $ ($ 1 \leq t \leq 1000 $) — 测试用例的数量。每个测试用例的描述如下。

每个测试用例的一行包含两个整数 $ n $ 和 $ m $ ($ 1 \leq n, m \leq 10^4 $) — 分别是表 $ a $ 的行数和列数。

## 输出格式
对于每个测试用例，输出一个整数 — 从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。

## 样例
### 输入示例 #1
```
7
1 1
2 3
3 2
7 1
1 10
5 5
10000 10000
```
### 输出示例 #1
```
1
12
13
28
55
85
500099995000
```

## 提示
在第一个测试用例中，唯一可能的路径由单个单元格 $ (1, 1) $ 组成。

第二个测试用例中成本最低的路径在题目描述中显示。

在第四和第五个测试用例中，从 $ (1, 1) $ 到 $ (n, m) $ 只有一条路径。两条路径都访问表中的每个单元格。**最优路径** ## 题目描述 给定一个大小为 $ n \times m $ 的表 $ a $。表的行从上到下编号为 $ 1 $ 到 $ n $，列从左到右编号为 $ 1 $ 到 $ m $。单元格 $ (i, j) $ 中的数字为 $ (i - 1) \cdot m + j $，即 $ a_{ij} = (i - 1) \cdot m + j $。 一只乌龟最初位于单元格 $ (1, 1) $，它想要到达单元格 $ (n, m) $。从单元格 $ (i, j) $，它可以一步转移到单元格 $ (i + 1, j) $ 或 $ (i, j + 1) $（如果存在的话）。路径是单元格的序列，对于序列中的每两个相邻单元格，满足乌龟可以一步从第一个单元格到达第二个单元格的条件。路径的成本是路径单元格中数字的总和。 例如，当 $ n = 2 $ 和 $ m = 3 $ 时，表如下所示。乌龟可以走以下路径：$ (1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) $。这条路径的成本等于 $ a_{11} + a_{12} + a_{13} + a_{23} = 12 $。另一方面，路径 $ (1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1) $ 和 $ (1, 1) \rightarrow (1, 3) $ 是不正确的，因为在第一条路径中乌龟不能迈出一步 $ (2, 2) \rightarrow (2, 1) $，而在第二条路径中它不能迈出一步 $ (1, 1) \rightarrow (1, 3) $。 要求告诉乌龟从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。注意，单元格 $ (1, 1) $ 和 $ (n, m) $ 是路径的一部分。 ## 输入格式 第一行包含一个整数 $ t $ ($ 1 \leq t \leq 1000 $) — 测试用例的数量。每个测试用例的描述如下。 每个测试用例的一行包含两个整数 $ n $ 和 $ m $ ($ 1 \leq n, m \leq 10^4 $) — 分别是表 $ a $ 的行数和列数。 ## 输出格式 对于每个测试用例，输出一个整数 — 从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。 ## 样例 ### 输入示例 #1 ``` 7 1 1 2 3 3 2 7 1 1 10 5 5 10000 10000 ``` ### 输出示例 #1 ``` 1 12 13 28 55 85 500099995000 ``` ## 提示 在第一个测试用例中，唯一可能的路径由单个单元格 $ (1, 1) $ 组成。 第二个测试用例中成本最低的路径在题目描述中显示。 在第四和第五个测试用例中，从 $ (1, 1) $ 到 $ (n, m) $ 只有一条路径。两条路径都访问表中的每个单元格。