309485: CF1687B. Railway System
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Railway System
题意翻译
> 进步?虽然根据所言所指的内容会有所不同,不过关于技术方面是幻想乡所无法比拟呢。——八坂神奈子,《东方求闻口授》 **这是一道交互题。** 在八坂神奈子和守矢神社的监督之下,幻想乡内的铁路系统 GSKR 取得了成功。它包含着 $n$ 个站点和 $m$ 条双向的铁路道路相连,第 $i$ 条道路有一个长度 $l_i(1 \leq l_i \leq 10^6)$。由于预算限制,这个铁路系统可能并不是联通的。两个站点之间也有可能有多条铁路道路直接相连。 一个铁路系统的总价值是它上面所有道路的长度之和,而一个铁路系统的容量的最大(最小)值等同于其最大(最小)权的极大生成森林的总价值。其中,极大生成森林指的是一个连通性与原图相同的生成森林。 现在神奈子有一个模拟装置,它可以产生不超过 $2m$ 次询问,每次询问输入一个长度为 $m$ 的字符串 $s$(仅由 $0$ 或 $1$ 构成),其中当 $s_i=1$ 的时候,这个模拟装置会假定第 $i$ 条铁路道路是可以使用的。这个模拟装置会告诉神奈子这个铁路系统的最大容量。 神奈子希望借助这个模拟装置,知道如果每一条铁路道路都能使用上的话,那么铁路系统的最小容量会是多少。 这个铁路系统的结构是已定的,换而言之,交互库并非自适应。 **输入格式** 输入一行正整数 $n$ 和 $m$($2 \leq n \leq 200$,$1 \leq m \leq 500$)。 **交互格式** 如果你需要作出一次询问的话,向标准输出输出一行 `? s`,其中 $s$ 是一个长度为 $m$ 的仅由 $0$ 或 $1$ 构成的字符串。接着从标准输入读入一行表示最大容量。 如果你进行了不合法的询问或者超出了询问次数上限,则你的程序会被判作 Wrong Answer。 如果你需要作出最后的回答,那么向标准输出输出一行 `! L`,其中 $L$ 指的铁路系统的最小容量会是多少。是这一步不会被计入到 $2m$ 次操作的上限。 在每一次查询之后,请不要忘记刷新缓冲区,否则你的程序会被判作 Idleness limit exceeded。题目描述
As for the technology in the outside world, it is really too advanced for Gensokyo to even look up to. —Yasaka Kanako, Symposium of Post-mysticism This is an interactive problem. Under the direct supervision of Kanako and the Moriya Shrine, the railway system of Gensokyo is finally finished. GSKR (Gensokyo Railways) consists of $ n $ stations with $ m $ bidirectional tracks connecting them. The $ i $ -th track has length $ l_i $ ( $ 1\le l_i\le 10^6 $ ). Due to budget limits, the railway system may not be connected, though there may be more than one track between two stations. The value of a railway system is defined as the total length of its all tracks. The maximum (or minimum) capacity of a railway system is defined as the maximum (or minimum) value among all of the currently functional system's [full spanning forest](https://en.wikipedia.org/wiki/Spanning_tree#Spanning_forests). In brief, full spanning forest of a graph is a spanning forest with the same connectivity as the given graph. Kanako has a simulator only able to process no more than $ 2m $ queries. The input of the simulator is a string $ s $ of length $ m $ , consisting of characters 0 and/or 1. The simulator will assume the $ i $ -th track functional if $ s_i= $ 1. The device will then tell Kanako the maximum capacity of the system in the simulated state. Kanako wants to know the the minimum capacity of the system with all tracks functional with the help of the simulator. The structure of the railway system is fixed in advance. In other words, the interactor is not adaptive.输入输出格式
输入格式
The first and only line of input contains two integers $ n,m $ ( $ 2 \leq n \leq 200 $ , $ 1\le m \le 500 $ ) — the number of stations and tracks.
输出格式
Begin the interaction by reading $ n,m $ . To make a query, print "? $ s $ " (without quotes, $ s $ is a string of length $ m $ , consisting of characters 0 and/or 1). Then you should read our response from standard input — the maximum capacity of the system in the simulated state. If your program has made an invalid query or has run out of tries, the interactor will terminate immediately and your program will get a verdict Wrong answer. To give the final answer, print "! $ L $ " (without the quotes, $ L $ is the minimum capacity of the system with all tracks functional). Note that giving this answer is not counted towards the limit of $ 2m $ queries. After printing a query do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use: - fflush(stdout) or cout.flush() in C++; - System.out.flush() in Java; - flush(output) in Pascal; - stdout.flush() in Python; - see documentation for other languages. Hacks The first line of input must contain two integers $ n,m $ ( $ 2 \leq n \leq 200 $ , $ 1\le m \le 500 $ ) — the number of stations and tracks. The next $ m $ lines of input must contain exactly $ 3 $ space-separated integers $ u_i $ , $ v_i $ , $ l_i $ ( $ 1\le u_i,v_i \le n $ , $ u_i\ne v_i $ , $ 1 \leq l_i \leq 10^6 $ ) — the endpoints and the length of the $ i $ -th track.
输入输出样例
输入样例 #1
5 4
0
5
9
7输出样例 #1
? 0000
? 1110
? 1111
? 1101
! 7说明
Here is the graph of the example, satisfying $ l_i=i $ . 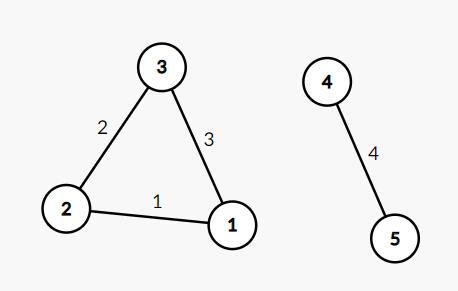Input
题意翻译
> 进步?虽然根据所言所指的内容会有所不同,不过关于技术方面是幻想乡所无法比拟呢。——八坂神奈子,《东方求闻口授》 **这是一道交互题。** 在八坂神奈子和守矢神社的监督之下,幻想乡内的铁路系统 GSKR 取得了成功。它包含着 $n$ 个站点和 $m$ 条双向的铁路道路相连,第 $i$ 条道路有一个长度 $l_i(1 \leq l_i \leq 10^6)$。由于预算限制,这个铁路系统可能并不是联通的。两个站点之间也有可能有多条铁路道路直接相连。 一个铁路系统的总价值是它上面所有道路的长度之和,而一个铁路系统的容量的最大(最小)值等同于其最大(最小)权的极大生成森林的总价值。其中,极大生成森林指的是一个连通性与原图相同的生成森林。 现在神奈子有一个模拟装置,它可以产生不超过 $2m$ 次询问,每次询问输入一个长度为 $m$ 的字符串 $s$(仅由 $0$ 或 $1$ 构成),其中当 $s_i=1$ 的时候,这个模拟装置会假定第 $i$ 条铁路道路是可以使用的。这个模拟装置会告诉神奈子这个铁路系统的最大容量。 神奈子希望借助这个模拟装置,知道如果每一条铁路道路都能使用上的话,那么铁路系统的最小容量会是多少。 这个铁路系统的结构是已定的,换而言之,交互库并非自适应。 **输入格式** 输入一行正整数 $n$ 和 $m$($2 \leq n \leq 200$,$1 \leq m \leq 500$)。 **交互格式** 如果你需要作出一次询问的话,向标准输出输出一行 `? s`,其中 $s$ 是一个长度为 $m$ 的仅由 $0$ 或 $1$ 构成的字符串。接着从标准输入读入一行表示最大容量。 如果你进行了不合法的询问或者超出了询问次数上限,则你的程序会被判作 Wrong Answer。 如果你需要作出最后的回答,那么向标准输出输出一行 `! L`,其中 $L$ 指的铁路系统的最小容量会是多少。是这一步不会被计入到 $2m$ 次操作的上限。 在每一次查询之后,请不要忘记刷新缓冲区,否则你的程序会被判作 Idleness limit exceeded。Output
**题目大意:**
这是一个交互问题。
在八坂神奈子和守矢神社的监督下,幻想乡的铁路系统GSKR终于完成了。GSKR由n个站点和m条双向轨道组成,第i条轨道长度为\(l_i\)(\(1 \leq l_i \leq 10^6\))。由于预算限制,铁路系统可能不是连通的,两个站点之间也可能有多条轨道直接相连。
一个铁路系统的价值定义为它所有轨道的总长度。铁路系统的最大(或最小)容量定义为所有当前可用的系统[全生成森林](https://en.wikipedia.org/wiki/Spanning_tree#Spanning_forests)的最大(**题目大意:** 这是一个交互问题。 在八坂神奈子和守矢神社的监督下,幻想乡的铁路系统GSKR终于完成了。GSKR由n个站点和m条双向轨道组成,第i条轨道长度为\(l_i\)(\(1 \leq l_i \leq 10^6\))。由于预算限制,铁路系统可能不是连通的,两个站点之间也可能有多条轨道直接相连。 一个铁路系统的价值定义为它所有轨道的总长度。铁路系统的最大(或最小)容量定义为所有当前可用的系统[全生成森林](https://en.wikipedia.org/wiki/Spanning_tree#Spanning_forests)的最大(
这是一个交互问题。
在八坂神奈子和守矢神社的监督下,幻想乡的铁路系统GSKR终于完成了。GSKR由n个站点和m条双向轨道组成,第i条轨道长度为\(l_i\)(\(1 \leq l_i \leq 10^6\))。由于预算限制,铁路系统可能不是连通的,两个站点之间也可能有多条轨道直接相连。
一个铁路系统的价值定义为它所有轨道的总长度。铁路系统的最大(或最小)容量定义为所有当前可用的系统[全生成森林](https://en.wikipedia.org/wiki/Spanning_tree#Spanning_forests)的最大(**题目大意:** 这是一个交互问题。 在八坂神奈子和守矢神社的监督下,幻想乡的铁路系统GSKR终于完成了。GSKR由n个站点和m条双向轨道组成,第i条轨道长度为\(l_i\)(\(1 \leq l_i \leq 10^6\))。由于预算限制,铁路系统可能不是连通的,两个站点之间也可能有多条轨道直接相连。 一个铁路系统的价值定义为它所有轨道的总长度。铁路系统的最大(或最小)容量定义为所有当前可用的系统[全生成森林](https://en.wikipedia.org/wiki/Spanning_tree#Spanning_forests)的最大(