Tokitsukaze and Meeting

题意翻译

#### 【题目翻译】 Tokitsukaze 正在安排一场学生会议。会议厅的座位是一个 $n$ 行 $m$ 列的矩形。 一共有 $(n \times m)$ 个学生参加会议，这些学生被从 $1$ 到 $(n \times m)$ 编号。这 $(n \times m)$ 个学生中有一些学生比较调皮，有些学生比较严肃。 学生将以编号从小到大的顺序进场。每个学生进场后将会坐在第 $1$ 行第 $1$ 列，而原本的学生将会后退一格，即： - 原本在第 $i$ 行第 $j$ 列的学生（$1 \leq j \leq m-1$），将会坐到第 $i$ 行第 $(j+1)$ 列； - 原本在第 $i$ 行第 $m$ 列的学生将会坐到第 $(i+1)$ 行第 $1$ 列。 （具体的过程请看原题面里的图片） 如果某一行或某一列有至少一位严肃的学生，那么这一行或这一列就会认为是好的行货好的列。 对于所有的 $1 \leq i \leq (n \cdot m)$，求当第 $i$ 位学生（即编号为 $i$ 的学生）进场后，好的行及好的列的数量的和。 #### 【输入格式】 **多组数据**。 第一行一个整数 $T$，表示数据的组数。 对于每组数据，第一行两个整数 $n,m$。 第二行是一个长为 $(n \cdot m)$ 的字符串 $s$，$s$ 只由 `0` 和 `1` 组成。如果 $s_{i}$ 为 `0`，则表示编号为 $i$ 的学生很调皮；如果 $s_{i}$ 为 `1`，则表示编号为 $i$ 的学生很严肃。 #### 【输出格式】 对于每组数据，输出一行共 $(n \cdot m)$ 个整数，表示当第 $i$ 位学生进场后，好的行及好的列的数量。 #### 【数据范围】 - $1 \leq T \leq 1 \times 10^{4}$ - $1 \leq n,m \leq 1 \times 10^{6},1 \leq (n \cdot m) \leq 1 \times 10^{6}$ - $1 \leq \sum (n \cdot m) \leq 1\times 10^{6}$ Translated by @HPXXZYY

题目描述

Tokitsukaze is arranging a meeting. There are $ n $ rows and $ m $ columns of seats in the meeting hall. There are exactly $ n \cdot m $ students attending the meeting, including several naughty students and several serious students. The students are numerated from $ 1 $ to $ n\cdot m $ . The students will enter the meeting hall in order. When the $ i $ -th student enters the meeting hall, he will sit in the $ 1 $ -st column of the $ 1 $ -st row, and the students who are already seated will move back one seat. Specifically, the student sitting in the $ j $ -th ( $ 1\leq j \leq m-1 $ ) column of the $ i $ -th row will move to the $ (j+1) $ -th column of the $ i $ -th row, and the student sitting in $ m $ -th column of the $ i $ -th row will move to the $ 1 $ -st column of the $ (i+1) $ -th row. For example, there is a meeting hall with $ 2 $ rows and $ 2 $ columns of seats shown as below: There will be $ 4 $ students entering the meeting hall in order, represented as a binary string "1100", of which '0' represents naughty students and '1' represents serious students. The changes of seats in the meeting hall are as follows: 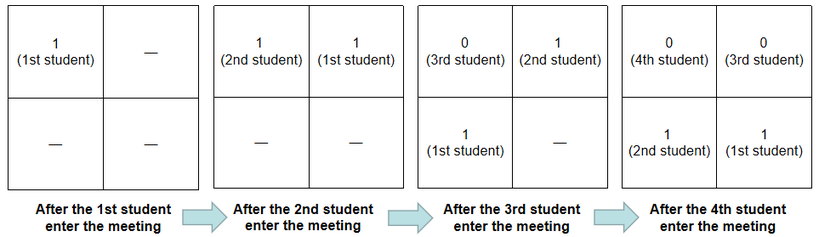Denote a row or a column good if and only if there is at least one serious student in this row or column. Please predict the number of good rows and columns just after the $ i $ -th student enters the meeting hall, for all $ i $ .

输入输出格式

输入格式

The first contains a single positive integer $ t $ ( $ 1 \leq t \leq 10\,000 $ ) — the number of test cases. For each test case, the first line contains two integers $ n $ , $ m $ ( $ 1 \leq n,m \leq 10^6 $ ; $ 1 \leq n \cdot m \leq 10^6 $ ), denoting there are $ n $ rows and $ m $ columns of seats in the meeting hall. The second line contains a binary string $ s $ of length $ n \cdot m $ , consisting only of zeros and ones. If $ s_i $ equal to '0' represents the $ i $ -th student is a naughty student, and $ s_i $ equal to '1' represents the $ i $ -th student is a serious student. It is guaranteed that the sum of $ n \cdot m $ over all test cases does not exceed $ 10^6 $ .

输出格式

For each test case, print a single line with $ n \cdot m $ integers — the number of good rows and columns just after the $ i $ -th student enters the meeting hall.

输入输出样例

输入样例 #1

3
2 2
1100
4 2
11001101
2 4
11001101

输出样例 #1

2 3 4 3
2 3 4 3 5 4 6 5
2 3 3 3 4 4 4 5

说明

The first test case is shown in the statement. After the $ 1 $ -st student enters the meeting hall, there are $ 2 $ good rows and columns: the $ 1 $ -st row and the $ 1 $ -st column. After the $ 2 $ -nd student enters the meeting hall, there are $ 3 $ good rows and columns: the $ 1 $ -st row, the $ 1 $ -st column and the $ 2 $ -nd column. After the $ 3 $ -rd student enters the meeting hall, the $ 4 $ rows and columns are all good. After the $ 4 $ -th student enters the meeting hall, there are $ 3 $ good rows and columns: the $ 2 $ -nd row, the $ 1 $ -st column and the $ 2 $ -nd column.