309424: CF1676G. White-Black Balanced Subtrees
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:9
Solved:0
Description
White-Black Balanced Subtrees
题意翻译
给定一棵 $n$ 个结点的树,根结点是 $1$,每个结点是黑色或白色的。 如果一棵树中黑色结点与白色结点数量相同,那么这棵树是“平衡的"。 问这棵 $n$ 个结点的树有多少棵“平衡的”子树。题目描述
You are given a rooted tree consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . The root is vertex $ 1 $ . There is also a string $ s $ denoting the color of each vertex: if $ s_i = \texttt{B} $ , then vertex $ i $ is black, and if $ s_i = \texttt{W} $ , then vertex $ i $ is white. A subtree of the tree is called balanced if the number of white vertices equals the number of black vertices. Count the number of balanced subtrees. A tree is a connected undirected graph without cycles. A rooted tree is a tree with a selected vertex, which is called the root. In this problem, all trees have root $ 1 $ . The tree is specified by an array of parents $ a_2, \dots, a_n $ containing $ n-1 $ numbers: $ a_i $ is the parent of the vertex with the number $ i $ for all $ i = 2, \dots, n $ . The parent of a vertex $ u $ is a vertex that is the next vertex on a simple path from $ u $ to the root. The subtree of a vertex $ u $ is the set of all vertices that pass through $ u $ on a simple path to the root. For example, in the picture below, $ 7 $ is in the subtree of $ 3 $ because the simple path $ 7 \to 5 \to 3 \to 1 $ passes through $ 3 $ . Note that a vertex is included in its subtree, and the subtree of the root is the entire tree. 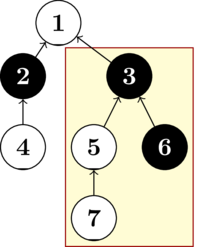 The picture shows the tree for $ n=7 $ , $ a=[1,1,2,3,3,5] $ , and $ s=\texttt{WBBWWBW} $ . The subtree at the vertex $ 3 $ is balanced.输入输出格式
输入格式
The first line of input contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains an integer $ n $ ( $ 2 \le n \le 4000 $ ) — the number of vertices in the tree. The second line of each test case contains $ n-1 $ integers $ a_2, \dots, a_n $ ( $ 1 \le a_i < i $ ) — the parents of the vertices $ 2, \dots, n $ . The third line of each test case contains a string $ s $ of length $ n $ consisting of the characters $ \texttt{B} $ and $ \texttt{W} $ — the coloring of the tree. It is guaranteed that the sum of the values $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case, output a single integer — the number of balanced subtrees.
输入输出样例
输入样例 #1
3
7
1 1 2 3 3 5
WBBWWBW
2
1
BW
8
1 2 3 4 5 6 7
BWBWBWBW输出样例 #1
2
1
4