Playoff

题意翻译

### 题目描述 考虑一个有 $2^n$ 个运动员参加的比赛，运动员的编号从1到 $2^n$。 比赛分 $n$ 个阶段举行。在每个阶段，运动员被按编号分成两人一组。在每一组中，运动员相互竞争，其中只有一人获胜。每组选手中的获胜者进入下一阶段，重新编号，被击败的运动员被淘汰出局。 当编号为 $x$ 的运动员和编号为 $y$ 的运动员比赛时，优胜者的决定如下： - 如果 $x+y$ 是奇数，则指数较低的运动员获胜（即，如果 $x<y$ ，则 $x$ 获胜，进入下一轮，否则 $y$ 获胜； - 如果 $x+y$ 是偶数，则指数较高的运动员获胜。 下图描述了当 $n=3$ 的比赛方式 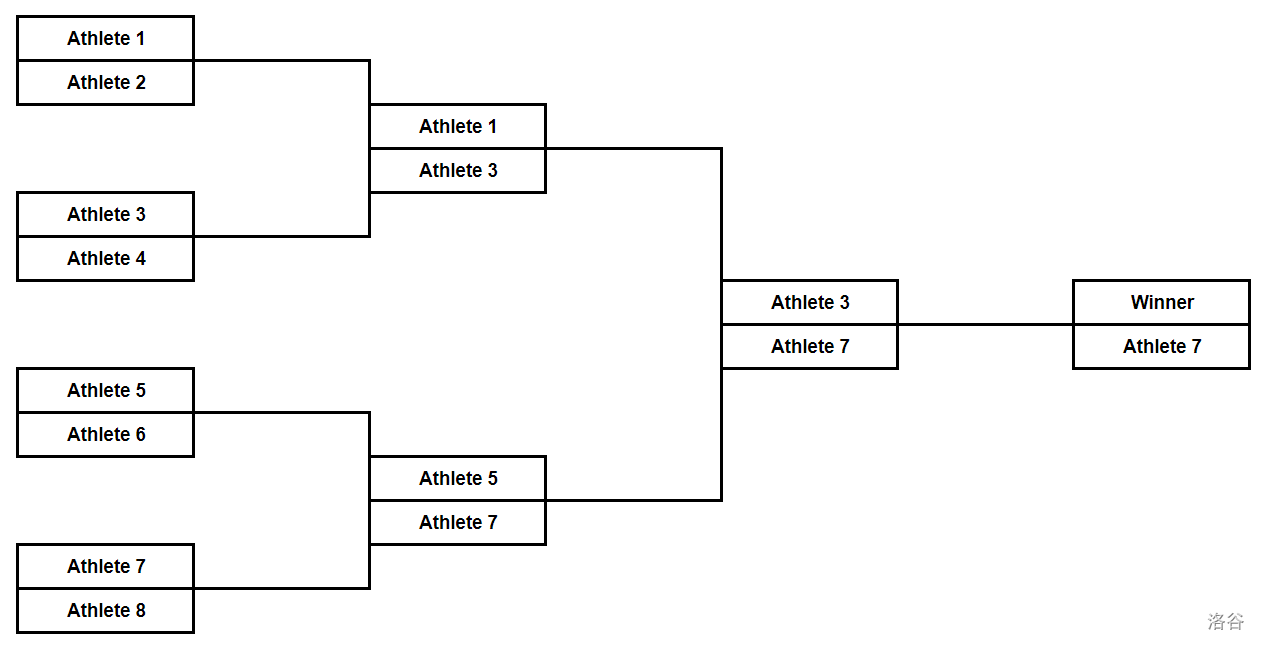 ### 输入格式 第一行包含一个整数 $T$ （ $1≤T≤30$ ）,表示测试样例的数量。 每个测试样例由一行组成，其中包含一个整数 $n$ （ $1≤n≤30$ )。 ### 输出格式 对于每个测试样例，输出一个整数（比赛冠军最开始的编号）。

题目描述

Consider a playoff tournament where $ 2^n $ athletes compete. The athletes are numbered from $ 1 $ to $ 2^n $ . The tournament is held in $ n $ stages. In each stage, the athletes are split into pairs in such a way that each athlete belongs exactly to one pair. In each pair, the athletes compete against each other, and exactly one of them wins. The winner of each pair advances to the next stage, the athlete who was defeated gets eliminated from the tournament. The pairs are formed as follows: - in the first stage, athlete $ 1 $ competes against athlete $ 2 $ ; $ 3 $ competes against $ 4 $ ; $ 5 $ competes against $ 6 $ , and so on; - in the second stage, the winner of the match " $ 1 $ – $ 2 $ " competes against the winner of the match " $ 3 $ – $ 4 $ "; the winner of the match " $ 5 $ – $ 6 $ " competes against the winner of the match " $ 7 $ – $ 8 $ ", and so on; - the next stages are held according to the same rules. When athletes $ x $ and $ y $ compete, the winner is decided as follows: - if $ x+y $ is odd, the athlete with the lower index wins (i. e. if $ x < y $ , then $ x $ wins, otherwise $ y $ wins); - if $ x+y $ is even, the athlete with the higher index wins. The following picture describes the way the tournament with $ n = 3 $ goes. 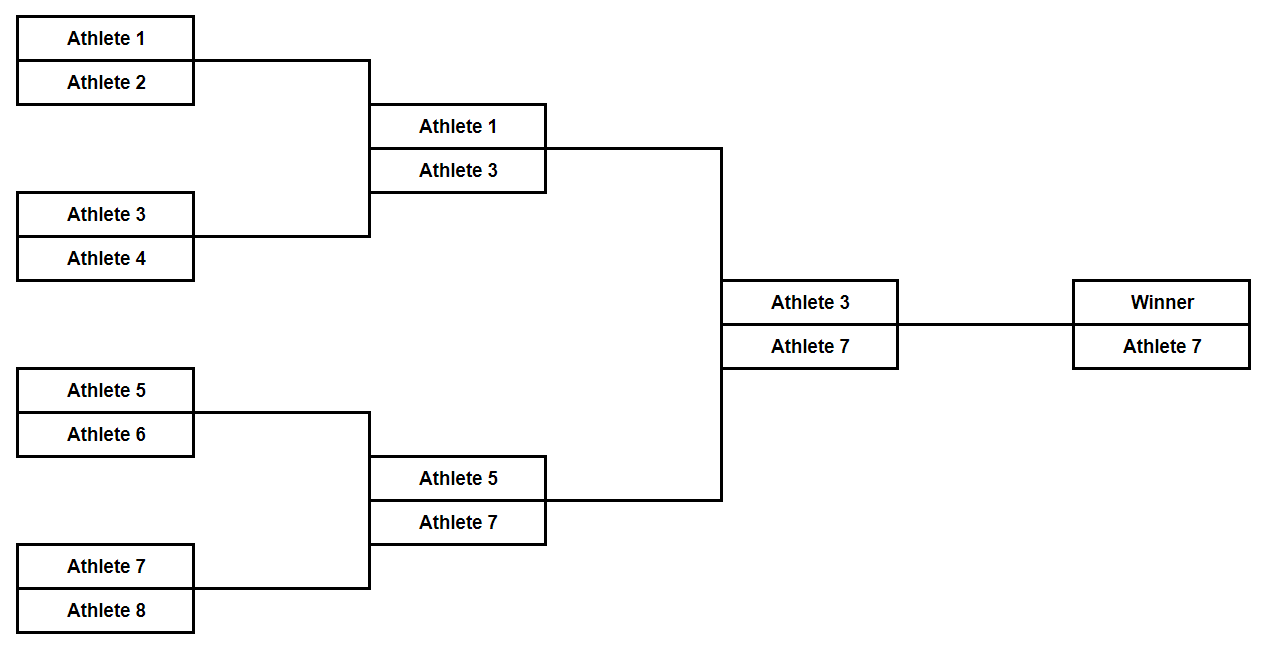Your task is the following one: given the integer $ n $ , determine the index of the athlete who wins the tournament.

输入输出格式

输入格式

The first line contains one integer $ t $ ( $ 1 \le t \le 30 $ ) — the number of test cases. Each test case consists of one line containing one integer $ n $ ( $ 1 \le n \le 30 $ ).

输出格式

For each test case, print one integer — the index of the winner of the tournament.

输入输出样例

输入样例 #1

2
3
1

输出样例 #1

7
1

说明

The case $ n = 3 $ is shown in the picture from the statement. If $ n = 1 $ , then there's only one match between athletes $ 1 $ and $ 2 $ . Since $ 1 + 2 = 3 $ is an odd number, the athlete with the lower index wins. So, the athlete $ 1 $ is the winner.