Hard Way

题意翻译

# 题面简述 Sam 住在 Awesomeburg，其市中心为三角形。 此外，三角形满足： - 它的顶点具有整数坐标。 - 它的顶点具有非负坐标。 - 它的顶点不会共线。 如果他可以从 X 轴的至少一个点沿着某条直线行走而不穿过三角形的内部，他就称市中心边界上的一个点（即三角形的边界）是安全的。 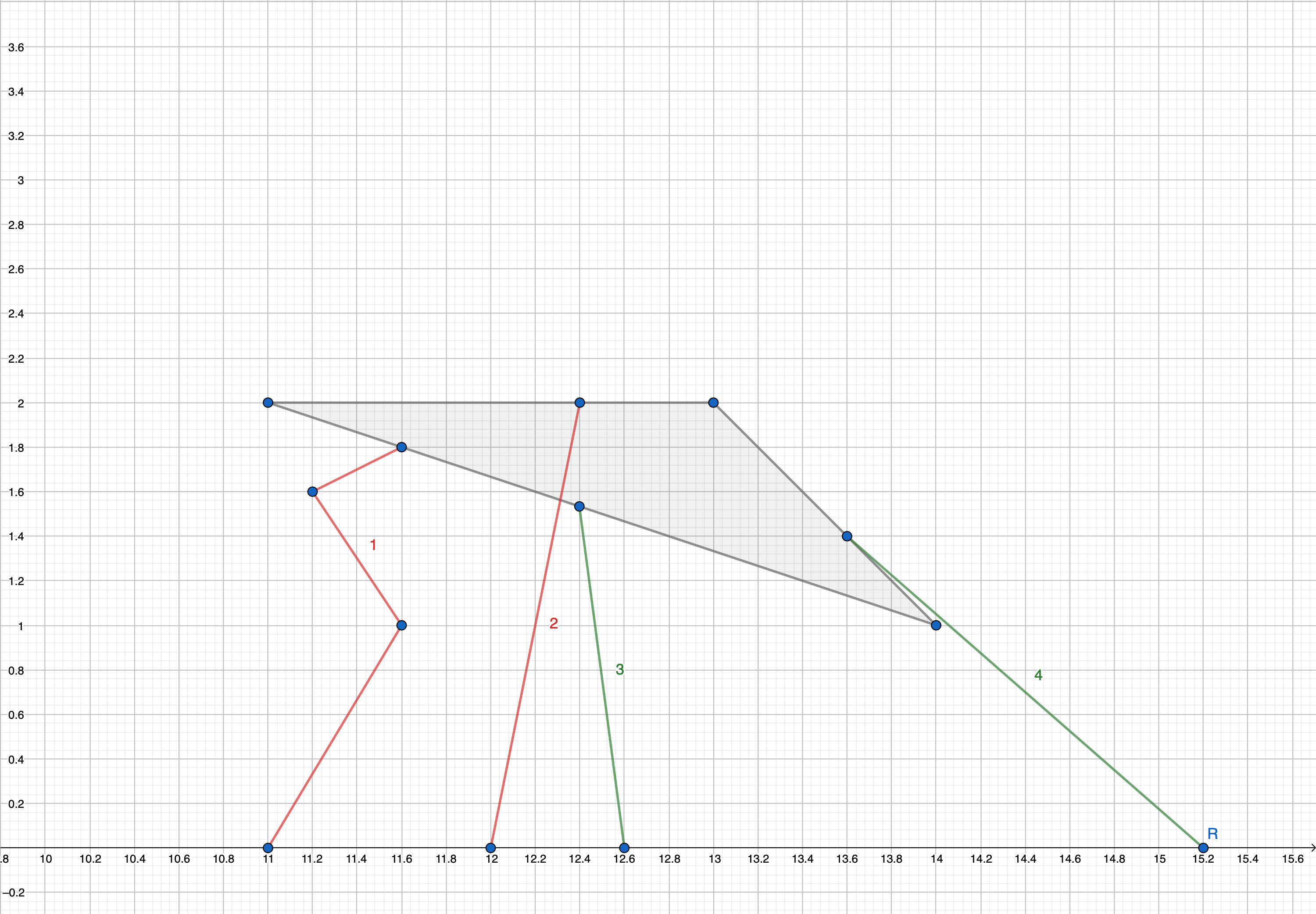 在图片中，市中心用灰色标记。 第一条路径无效，因为它不沿着直线走。 第二条路径无效，因为它与市中心的内部相交。 第三条和第四条路径是正确的。 求市区边界不安全部分的总长度。 可以证明，这些部分是段，它们的数量是有限的。 # 输入格式 每个测试包含多个测试用例。 第一行包含一个整数 $t$（$1 \le t \le 1000 $），表示测试用例的数量。每一组测试用例的描述如下： 每个测试用例包含三行，每行包含两个整数 $x, y$（$0 \le x_i, y_i \le 10^9$），表示市中心边界顶点的坐标。 # 输出格式 为每个测试用例输出问题的答案。 如果绝对或相对误差不超过 $10^{-9}$，则您的答案将被视为正确。

题目描述

Sam lives in Awesomeburg, its downtown has a triangular shape. Also, the following is true about the triangle: - its vertices have integer coordinates, - the coordinates of vertices are non-negative, and - its vertices are not on a single line. He calls a point on the downtown's border (that is the border of the triangle) safe if he can reach this point from at least one point of the line $ y = 0 $ walking along some straight line, without crossing the interior of the triangle. In the picture the downtown is marked with grey color. The first path is invalid because it does not go along a straight line. The second path is invalid because it intersects with the interior of the downtown. The third and fourth paths are correct.Find the total length of the unsafe parts of the downtown border. It can be proven that these parts are segments and their number is finite.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. Description of the test cases follows. Each test case contains three lines, each of them contains two integers $ x_i $ , $ y_i $ ( $ 0 \le x_i, y_i \le 10^9 $ ) — coordinates of the vertices of the downtown's border.

输出格式

For each test case print a single number — the answer to the problem. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-9} $ . Formally let your answer be $ a $ , jury answer be $ b $ . Your answer will be considered correct if $ \frac{|a - b|}{\max{(1, |b|)}} \le 10^{-9} $ .

输入输出样例

输入样例 #1

5
8 10
10 4
6 2
4 6
0 1
4 2
14 1
11 2
13 2
0 0
4 0
2 4
0 1
1 1
0 0

输出样例 #1

0.0000000
0
2.0000
0.00
1

说明

In the picture, the downtowns of the first three test cases are illustrated. Triangles are enumerated according to the indices of test cases they belong to. In the first two test cases, all points on the borders of the downtowns are safe, thus the answers are $ 0 $ . In the following picture unsafe points for the third test case are marked with black color: In the fourth test case, all points on the border of the downtown are safe.

题意翻译

# 题面简述 Sam 住在 Awesomeburg，其市中心为三角形。 此外，三角形满足： - 它的顶点具有整数坐标。 - 它的顶点具有非负坐标。 - 它的顶点不会共线。 如果他可以从 X 轴的至少一个点沿着某条直线行走而不穿过三角形的内部，他就称市中心边界上的一个点（即三角形的边界）是安全的。  在图片中，市中心用灰色标记。 第一条路径无效，因为它不沿着直线走。 第二条路径无效，因为它与市中心的内部相交。 第三条和第四条路径是正确的。 求市区边界不安全部分的总长度。 可以证明，这些部分是段，它们的数量是有限的。 # 输入格式 每个测试包含多个测试用例。 第一行包含一个整数 $t$（$1 \le t \le 1000 $），表示测试用例的数量。每一组测试用例的描述如下： 每个测试用例包含三行，每行包含两个整数 $x, y$（$0 \le x_i, y_i \le 10^9$），表示市中心边界顶点的坐标。 # 输出格式 为每个测试用例输出问题的答案。 如果绝对或相对误差不超过 $10^{-9}$，则您的答案将被视为正确。