Dragon Curve

题意翻译

一条龙形曲线是一个自相似分形曲线。在这道题中，这是一条由相同长度的直线段连成直角形成的曲线。一个构造龙形曲线的简单方式如下：取一长条状纸，沿相同方向对折 $n$ 次，然后部分展开它，使得这些线段两两呈直角。这个过程描述如下： （图） 在这个例子中，构造了一条阶为 $3$ 的龙形曲线。通常来说，高阶龙形曲线会以低阶龙形曲线为前缀。这允许我们定义无限阶的龙形曲线，即有限阶龙形曲线，当阶趋于无穷时的情况。 考虑四条无限阶龙形曲线。每条都是从原点（点 $(0,0)$）出发的，并且每条线段的长度都是 $\sqrt 2$。四条曲线第一条线段的终点分别为 $(1,1),(-1,1),(-1,-1)$ 和 $(1,-1)$。每条曲线第一次都向左转（这意味着，第一条曲线上的第二条线段终点为 $(0,2)$）。在这种情况下，每条线段都是某个与坐标平行，且顶点坐标为整数的单位正方形的对角线，并且可以证明，恰好有一条线段经过每个这样的正方形。 给定一个点 $(x,y)$，你的任务是找出是哪条曲线穿过了两个对角坐标为 $(x,y)$ 和 $(x+1,y+1)$ 的方格，并且找出这条线段在曲线上的位置。曲线编号为 $1$ 到 $4$。曲线 $1$ 经过 $(1,1)$，曲线 $2$ 经过 $(-1,1)$，曲线 $3$ 经过 $(-1,-1)$，曲线 $4$ 经过 $(1,-1)$。曲线上的线段都从 $1$ 开始编号。 第一行一个整数 $n\ (1\le n\le 2\cdot 10^5)$，表示测试数据组数。 接下来 $n$ 行，每行两个整数 $x,y\ (-10^9\le x,y\le 10^9)$，表示每次询问的坐标。 对于每组数据，输出两个整数。第一个整数表示曲线的编号（$1$ 到 $4$ 之间的整数，包括两端），第二个数是线段在曲线上的位置（曲线上的线段都从 $1$ 开始编号）。 你可以用如下图片来调试你的程序。 （图）

题目描述

A dragon curve is a self-similar fractal curve. In this problem, it is a curve that consists of straight-line segments of the same length connected at right angles. A simple way to construct a dragon curve is as follows: take a strip of paper, fold it in half $ n $ times in the same direction, then partially unfold it such that the segments are joined at right angles. This is illustrated here: 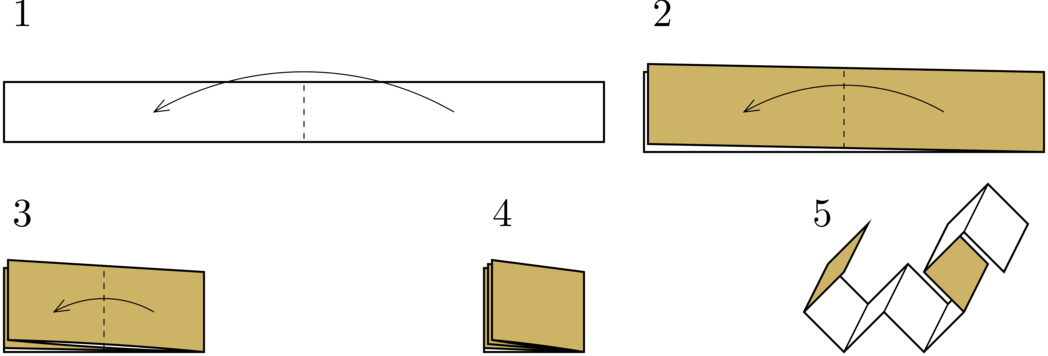In this example, a dragon curve of order $ 3 $ is constructed. In general, a dragon curve of a higher order will have a dragon curve of a lower order as its prefix. This allows us to define a dragon curve of infinite order, which is the limit of dragon curves of a finite order as the order approaches infinity. Consider four dragon curves of infinite order. Each starts at the origin (the point $ (0,0) $ ), and the length of each segment is $ \sqrt2 $ . The first segments of the curves end at the points $ (1,1) $ , $ (-1,1) $ , $ (-1,-1) $ and $ (1,-1) $ , respectively. The first turn of each curve is left (that is, the second segment of the first curve ends at the point $ (0,2) $ ). In this case, every segment is a diagonal of an axis-aligned unit square with integer coordinates, and it can be proven that there is exactly one segment passing through every such square. Given a point $ (x,y) $ , your task is to find on which of the four curves lies the segment passing through the square with the opposite corners at $ (x,y) $ and $ (x+1,y+1) $ , as well as the position of that segment on that curve. The curves are numbered $ 1 $ through $ 4 $ . Curve $ 1 $ goes through $ (1,1) $ , $ 2 $ through $ (-1,1) $ , $ 3 $ through $ (-1,-1) $ , and $ 4 $ through $ (1,-1) $ . The segments are numbered starting with $ 1 $ .

输入输出格式

输入格式

The first line contains an integer $ n $ ( $ 1\le n\le2\cdot10^5 $ ) — the number of test cases. Each of the following $ n $ lines contains two integers $ x $ and $ y $ ( $ -10^9\le x,y\le10^9 $ ) — the coordinates.

输出格式

For each test case, print a line containing two integers — the first is the index of the curve (an integer between $ 1 $ and $ 4 $ , inclusive), and the second is the position on the curve (the first segment has the position $ 1 $ ).

输入输出样例

输入样例 #1

5
0 0
-2 0
-7 -7
5 -9
9 9

输出样例 #1

1 1
2 2
3 189
4 186
2 68

说明

You can use this illustration to debug your solution: