Morning Jogging

题目描述

The 2050 volunteers are organizing the "Run! Chase the Rising Sun" activity. Starting on Apr 25 at 7:30 am, runners will complete the 6km trail around the Yunqi town. There are $ n+1 $ checkpoints on the trail. They are numbered by $ 0 $ , $ 1 $ , ..., $ n $ . A runner must start at checkpoint $ 0 $ and finish at checkpoint $ n $ . No checkpoint is skippable — he must run from checkpoint $ 0 $ to checkpoint $ 1 $ , then from checkpoint $ 1 $ to checkpoint $ 2 $ and so on. Look at the picture in notes section for clarification. Between any two adjacent checkpoints, there are $ m $ different paths to choose. For any $ 1\le i\le n $ , to run from checkpoint $ i-1 $ to checkpoint $ i $ , a runner can choose exactly one from the $ m $ possible paths. The length of the $ j $ -th path between checkpoint $ i-1 $ and $ i $ is $ b_{i,j} $ for any $ 1\le j\le m $ and $ 1\le i\le n $ . To test the trail, we have $ m $ runners. Each runner must run from the checkpoint $ 0 $ to the checkpoint $ n $ once, visiting all the checkpoints. Every path between every pair of adjacent checkpoints needs to be ran by exactly one runner. If a runner chooses the path of length $ l_i $ between checkpoint $ i-1 $ and $ i $ ( $ 1\le i\le n $ ), his tiredness is $ $\min_{i=1}^n l_i, $ $ i. e. the minimum length of the paths he takes.</p><p>Please arrange the paths of the $ m$ runners to minimize the sum of tiredness of them.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10\,000 $ ). Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \leq n,m \leq 100 $ ). The $ i $ -th of the next $ n $ lines contains $ m $ integers $ b_{i,1} $ , $ b_{i,2} $ , ..., $ b_{i,m} $ ( $ 1 \le b_{i,j} \le 10^9 $ ). It is guaranteed that the sum of $ n\cdot m $ over all test cases does not exceed $ 10^4 $ .

输出格式

For each test case, output $ n $ lines. The $ j $ -th number in the $ i $ -th line should contain the length of the path that runner $ j $ chooses to run from checkpoint $ i-1 $ to checkpoint $ i $ . There should be exactly $ m $ integers in the $ i $ -th line and these integers should form a permuatation of $ b_{i, 1} $ , ..., $ b_{i, m} $ for all $ 1\le i\le n $ . If there are multiple answers, print any.

输入输出样例

输入样例 #1

2
2 3
2 3 4
1 3 5
3 2
2 3
4 1
3 5

输出样例 #1

2 3 4
5 3 1
2 3
4 1
3 5

说明

In the first case, the sum of tiredness is $ \min(2,5) + \min(3,3) + \min(4,1) = 6 $ . 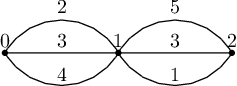In the second case, the sum of tiredness is $ \min(2,4,3) + \min(3,1,5) = 3 $ .