Hobbits

题意翻译

给出一条折线 $L$，折线由 $n$ 个点 $(x_1, y_1) \rightarrow \ldots \rightarrow (x_n, y_n)$ 构成，其中 $x_i < x_{i + 1}$。 在 $(x_n, y_n + H)$ 处有一个光源，向全方位发射光线。光线为直线，且遇到折线 $L$ 就会停止（即不会穿透）。 求折线 $L$ 上，被光照到部分的长度。

题目描述

The hobbits Frodo and Sam are carrying the One Ring to Mordor. In order not to be spotted by orcs, they decided to go through the mountains. The mountain relief can be represented as a polyline with $ n $ points $ (x_i, y_i) $ , numbered from $ 1 $ to $ n $ ( $ x_i < x_{i + 1} $ for $ 1 \le i \le n - 1 $ ). Hobbits start their journey at the point $ (x_1, y_1) $ and should reach the point $ (x_n, y_n) $ to complete their mission. The problem is that there is a tower with the Eye of Sauron, which watches them. The tower is located at the point $ (x_n, y_n) $ and has the height $ H $ , so the Eye is located at the point $ (x_n, y_n + H) $ . In order to complete the mission successfully, the hobbits have to wear cloaks all the time when the Sauron Eye can see them, i. e. when there is a direct line from the Eye to the hobbits which is not intersected by the relief. The hobbits are low, so their height can be considered negligibly small, but still positive, so when a direct line from the Sauron Eye to the hobbits only touches the relief, the Eye can see them. 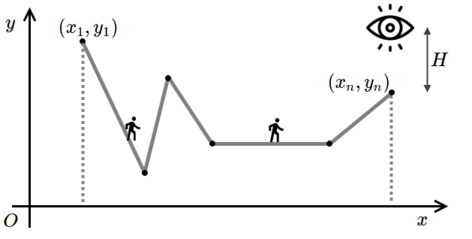The Sauron Eye can't see hobbits when they are in the left position, but can see them when they are in the right position.The hobbits do not like to wear cloaks, so they wear them only when they can be spotted by the Eye. Your task is to calculate the total distance the hobbits have to walk while wearing cloaks.

输入输出格式

输入格式

The first line of the input contains two integers $ n $ and $ H $ ( $ 2 \le n \le 2 \cdot 10^5 $ ; $ 1 \le H \le 10^4 $ ) — the number of vertices in polyline and the tower height. The next $ n $ lines contain two integers $ x_i, y_i $ each ( $ 0 \le x_i \le 4 \cdot 10^5 $ ; $ 0 \le y_i \le 10^4 $ ) — the coordinates of the polyline vertices. It is guaranteed that $ x_i < x_{i + 1} $ for $ 1 \le i \le n - 1 $ .

输出格式

Print one real number — the total distance the hobbits have to walk while wearing cloaks. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ — formally, if your answer is $ a $ , and the jury's answer is $ b $ , your answer will be accepted if $ \dfrac{|a - b|}{\max(1, b)} \le 10^{-6} $ .

输入输出样例

输入样例 #1

6 10
10 40
20 10
25 30
30 15
50 15
65 30

输出样例 #1

70.4034587602

输入样例 #2

9 5
0 0
5 10
15 10
20 0
25 11
30 0
35 10
50 10
60 5

输出样例 #2

27.2787986124

输入样例 #3

2 10000
0 10000
400000 0

输出样例 #3

400124.9804748512