Errich-Tac-Toe (Easy Version)

题意翻译

此题的简单版本与困难版本的不同只有困难版本的初始棋盘中含有 o 棋子，而简单版本没有。 这里有一个 $n$ 行 $n$ 列的井字棋棋盘，棋盘中的每一个格子要么是空的，要么包含一个棋子。 这里有两种棋子分别为 x 和 o 。如果有三个同种类的棋子连续横着或竖着排列，则称这是获胜局。（注意：斜着不算） 如果棋盘中没有这样的连续三个同种类的排列，则称这是一个平局。 在一次操作中，你可以将一个 x 棋子变为 o 棋子。令 $k$ 为初始棋盘中棋子的总数，你可以做最多 $\left\lfloor\dfrac{k}{3}\right\rfloor$ 次上述操作使得最后的局面为平局。注意：你不需要最小化操作次数。

题目描述

The only difference between the easy and hard versions is that tokens of type O do not appear in the input of the easy version. Errichto gave Monogon the following challenge in order to intimidate him from taking his top contributor spot on Codeforces. In a Tic-Tac-Toe grid, there are $ n $ rows and $ n $ columns. Each cell of the grid is either empty or contains a token. There are two types of tokens: X and O. If there exist three tokens of the same type consecutive in a row or column, it is a winning configuration. Otherwise, it is a draw configuration. 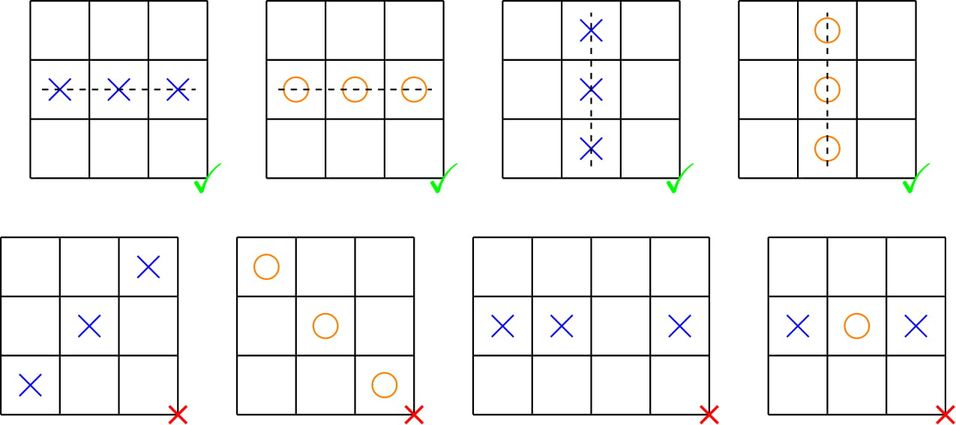 The patterns in the first row are winning configurations. The patterns in the second row are draw configurations. In an operation, you can change an X to an O, or an O to an X. Let $ k $ denote the total number of tokens in the grid. Your task is to make the grid a draw in at most $ \lfloor \frac{k}{3}\rfloor $ (rounding down) operations. You are not required to minimize the number of operations.

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1\le t\le 100 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1\le n\le 300 $ ) — the size of the grid. The following $ n $ lines each contain a string of $ n $ characters, denoting the initial grid. The character in the $ i $ -th row and $ j $ -th column is '.' if the cell is empty, or it is the type of token in the cell: 'X' or 'O'. It is guaranteed that not all cells are empty. In the easy version, the character 'O' does not appear in the input. The sum of $ n $ across all test cases does not exceed $ 300 $ .

输出格式

For each test case, print the state of the grid after applying the operations. We have proof that a solution always exists. If there are multiple solutions, print any.

输入输出样例

输入样例 #1

3
3
.X.
XXX
.X.
6
XX.XXX
XXXXXX
XXX.XX
XXXXXX
XX.X.X
XXXXXX
5
XXX.X
.X..X
XXX.X
..X..
..X..

输出样例 #1

.X.
XOX
.X.
XX.XXO
XOXXOX
OXX.XX
XOOXXO
XX.X.X
OXXOXX
XOX.X
.X..X
XXO.O
..X..
..X..

说明

In the first test case, there are initially three 'X' consecutive in the second row and the second column. By changing the middle token to 'O' we make the grid a draw, and we only changed $ 1\le \lfloor 5/3\rfloor $ token. In the second test case, we change only $ 9\le \lfloor 32/3\rfloor $ tokens, and there does not exist any three 'X' or 'O' consecutive in a row or column, so it is a draw. In the third test case, we change only $ 3\le \lfloor 12/3\rfloor $ tokens, and the resulting grid is a draw.