Rotary Laser Lock

题意翻译

### 题目描述 为了防止这些顽皮的兔子在动物园里自由游荡，动物园管理员为兔子圈设置了一个特殊的锁。这种锁叫做旋转激光锁。 - 锁由编号为 $0$ 到 $n−1$ 的 $n$ 个同心环组成。最里面的环是环 $0$，最外面的环是环 $n−1$。 - 所有环平均分成 $n\times m$ 部分。这些环中的每一个都包含一个金属圆弧，正好覆盖了 $m$ 个相邻的部分。 - 在环的中心是一个核心。有 $n\times m$ 接收器围绕着整个锁，对准 $n\times m$ 个部分。 - 核心有 $n\times m$ 个激光器，从中心中的每个部分向外照射。激光可以被任何一个电弧阻挡。锁外面的显示屏显示有多少激光击中了外部接收器。 （见上图） 在上例中，有 $n=3$ 个环，每个环覆盖 $m=4$ 个截面。弧线的颜色为绿色（环 $0$ ）、紫色（环 $1$ ）和蓝色（环$2$ ），而激光束显示为红色。 有 $n\times m=12$ 段，$3$ 个激光器没有被任何弧光阻挡，因此在这种情况下显示器将显示 $3$。 Wabbit 试图打开锁释放兔子，但锁是完全不透明的，他看不见任何弧线在哪里。如果给出弧的相对位置，Wabbit 可以自己打开锁。 准确地说，Wabbit需要 $n-1$ 个整数 $p_1，p_2，\ldots，p_{n-1}$ 作为相对位置，满足对于任意的 $1\leqslant i< n$，有 $0 \leqslant p_i\leqslant n\times m$。 Wabbit 要顺时针旋转环 $0$ 恰好 $p_i$ 次，使环 $0$ 覆盖的部分与环 $i$ 覆盖的部分完全对齐。 在上面的例子中，相对位置 $p_1=1,p_2=7$。 他可以选择 $n$ 个环中的任意一个，并将其顺时针或逆时针旋转 $1$ 段。每次旋转后，您将在显示屏上看到数字。 因为 Wabbit 的爪子很小，他让你帮他找到他所有的位置。在 Wabbit 失去耐心之前，你可以让他旋转最多 $15000$ 次。 ### 输入格式 第一行包含两个整数 $n$ 和 $m$ $(2\leqslant n \leqslant 100,2\leqslant m \leqslant 20)$，表示环的数量和每个环覆盖的部分的数量。 ### 输出格式 要执行旋转，请在输出一行 ``? x d``，满足 $(0\leqslant x <n),d\in\{-1,1\}$。 其中 $x$ 是你想要旋转的环，$d$ 是你想要旋转的方向。$ d=1 $表示顺时针旋转 $1$ 段，$d=-1$表示逆时针旋转 $1$ 段。 对于每个询问，你会得到一个整数 $a$，表示旋转完成后，没有被任何电弧阻挡的激光器数量。 一旦你计算出了弧的相对位置，输出一行 `! p[1] p[2] ... p[n-1]`。 注意环的位置是在每个测试点前确定的，不会自适应。

题目描述

This is an interactive problem. To prevent the mischievous rabbits from freely roaming around the zoo, Zookeeper has set up a special lock for the rabbit enclosure. This lock is called the Rotary Laser Lock. The lock consists of $ n $ concentric rings numbered from $ 0 $ to $ n-1 $ . The innermost ring is ring $ 0 $ and the outermost ring is ring $ n-1 $ . All rings are split equally into $ nm $ sections each. Each of those rings contains a single metal arc that covers exactly $ m $ contiguous sections. At the center of the ring is a core and surrounding the entire lock are $ nm $ receivers aligned to the $ nm $ sections. The core has $ nm $ lasers that shine outward from the center, one for each section. The lasers can be blocked by any of the arcs. A display on the outside of the lock shows how many lasers hit the outer receivers. 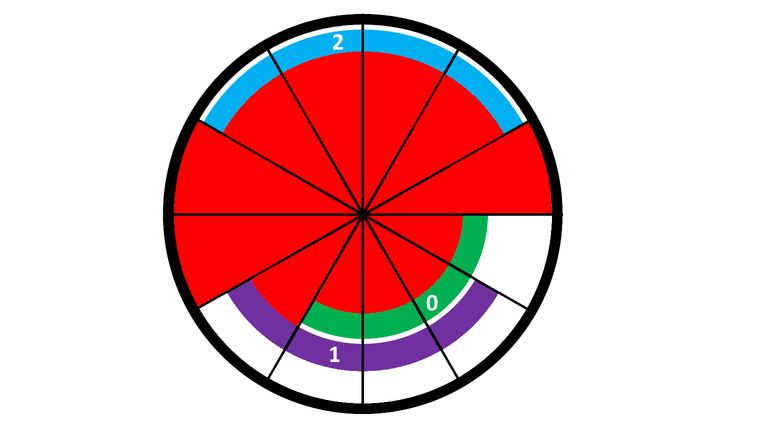In the example above, there are $ n=3 $ rings, each covering $ m=4 $ sections. The arcs are colored in green (ring $ 0 $ ), purple (ring $ 1 $ ), and blue (ring $ 2 $ ) while the lasers beams are shown in red. There are $ nm=12 $ sections and $ 3 $ of the lasers are not blocked by any arc, thus the display will show $ 3 $ in this case. Wabbit is trying to open the lock to free the rabbits, but the lock is completely opaque, and he cannot see where any of the arcs are. Given the relative positions of the arcs, Wabbit can open the lock on his own. To be precise, Wabbit needs $ n-1 $ integers $ p_1,p_2,\ldots,p_{n-1} $ satisfying $ 0 \leq p_i < nm $ such that for each $ i $ $ (1 \leq i < n) $ , Wabbit can rotate ring $ 0 $ clockwise exactly $ p_i $ times such that the sections that ring $ 0 $ covers perfectly aligns with the sections that ring $ i $ covers. In the example above, the relative positions are $ p_1 = 1 $ and $ p_2 = 7 $ . To operate the lock, he can pick any of the $ n $ rings and rotate them by $ 1 $ section either clockwise or anti-clockwise. You will see the number on the display after every rotation. Because his paws are small, Wabbit has asked you to help him to find the relative positions of the arcs after all of your rotations are completed. You may perform up to $ 15000 $ rotations before Wabbit gets impatient.

输入输出格式

输入格式

The first line consists of 2 integers $ n $ and $ m $ $ (2 \leq n \leq 100, 2 \leq m \leq 20) $ , indicating the number of rings and the number of sections each ring covers.

输出格式

To perform a rotation, print on a single line "? x d" where $ x $ $ (0 \leq x < n) $ is the ring that you wish to rotate and $ d $ $ (d \in \{-1,1\}) $ is the direction that you would like to rotate in. $ d=1 $ indicates a clockwise rotation by $ 1 $ section while $ d=-1 $ indicates an anticlockwise rotation by $ 1 $ section. For each query, you will receive a single integer $ a $ : the number of lasers that are not blocked by any of the arcs after the rotation has been performed. Once you have figured out the relative positions of the arcs, print ! followed by $ n-1 $ integers $ p_1, p_2, \ldots, p_{n-1} $ . Do note that the positions of the rings are predetermined for each test case and won't change during the interaction process. After printing a query do not forget to output the end of line and flush the output. Otherwise, you will get Idleness limit exceeded verdict. To do this, use: - fflush(stdout) or cout.flush() in C++; - System.out.flush() in Java; - flush(output) in Pascal; - stdout.flush() in Python; - see documentation for other languages. Hacks: To hack, use the following format of test: The first line should contain two integers $ n $ and $ m $ . The next line of should contain $ n-1 $ integers $ p_1,p_2,\ldots,p_{n-1} $ : relative positions of rings $ 1,2,\ldots,n-1 $ .

输入输出样例

输入样例 #1

3 4

4

4

3

输出样例 #1

? 0 1

? 2 -1

? 1 1

! 1 5

说明

For the first test, the configuration is the same as shown on the picture from the statement. After the first rotation (which is rotating ring $ 0 $ clockwise by $ 1 $ section), we obtain the following configuration: After the second rotation (which is rotating ring $ 2 $ counter-clockwise by $ 1 $ section), we obtain the following configuration: After the third rotation (which is rotating ring $ 1 $ clockwise by $ 1 $ section), we obtain the following configuration: If we rotate ring $ 0 $ clockwise once, we can see that the sections ring $ 0 $ covers will be the same as the sections that ring $ 1 $ covers, hence $ p_1=1 $ . If we rotate ring $ 0 $ clockwise five times, the sections ring $ 0 $ covers will be the same as the sections that ring $ 2 $ covers, hence $ p_2=5 $ . Note that if we will make a different set of rotations, we can end up with different values of $ p_1 $ and $ p_2 $ at the end.