Polygon

题意翻译

给定一个数n，生成一个n* n的一个全为0的初始矩阵，矩阵上方和下方均有一排炮台，矩阵的下边和右边是边界；炮台可以发射子弹，子弹只能直线行走，且遇到边界后会停止，遇到一个停止的子弹也会停止，子弹停止后的坐标里面的值记为1； ## 输入格式 一个T；表示有T组数据；每组数据都有一个n； 接下来是一个n* n的矩阵，里面的值只有0或1；问输入的这个矩阵能否由初始矩阵（全为0）通过炮台打出来；能则输出“YES”，否则输出“NO”

题目描述

Polygon is not only the best platform for developing problems but also a square matrix with side $ n $ , initially filled with the character 0. On the polygon, military training was held. The soldiers placed a cannon above each cell in the first row and a cannon to the left of each cell in the first column. Thus, exactly $ 2n $ cannons were placed. 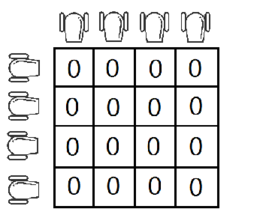Initial polygon for $ n=4 $ . Cannons shoot character 1. At any moment of time, no more than one cannon is shooting. When a 1 flies out of a cannon, it flies forward (in the direction of the shot) until it collides with a polygon border or another 1. After that, it takes the cell in which it was before the collision and remains there. Take a look at the examples for better understanding. More formally: - if a cannon stands in the row $ i $ , to the left of the first column, and shoots with a 1, then the 1 starts its flight from the cell ( $ i, 1 $ ) and ends in some cell ( $ i, j $ ); - if a cannon stands in the column $ j $ , above the first row, and shoots with a 1, then the 1 starts its flight from the cell ( $ 1, j $ ) and ends in some cell ( $ i, j $ ). For example, consider the following sequence of shots: 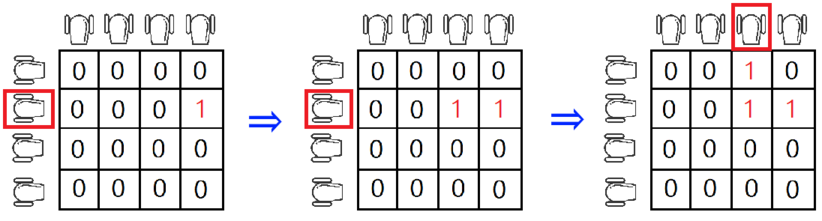 1. Shoot the cannon in the row $ 2 $ . 2. Shoot the cannon in the row $ 2 $ . 3. Shoot the cannon in column $ 3 $ . You have a report from the military training on your desk. This report is a square matrix with side length $ n $ consisting of 0 and 1. You wonder if the training actually happened. In other words, is there a sequence of shots such that, after the training, you get the given matrix? Each cannon can make an arbitrary number of shots. Before the training, each cell of the polygon contains 0.

输入输出格式

输入格式

The first line contains an integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. Then $ t $ test cases follow. Each test case starts with a line containing an integer $ n $ ( $ 1 \le n \le 50 $ ) — the size of the polygon. This is followed by $ n $ lines of length $ n $ , consisting of 0 and 1 — the polygon matrix after the training. The total area of the matrices in all test cases in one test does not exceed $ 10^5 $ .

输出格式

For each test case print: - YES if there is a sequence of shots leading to a given matrix; - NO if such a sequence does not exist. The letters in the words YES and NO can be printed in any case.

输入输出样例

输入样例 #1

5
4
0010
0011
0000
0000
2
10
01
2
00
00
4
0101
1111
0101
0111
4
0100
1110
0101
0111

输出样例 #1

YES
NO
YES
YES
NO

说明

The first test case was explained in the statement. The answer to the second test case is NO, since a 1 in a cell ( $ 1, 1 $ ) flying out of any cannon would continue its flight further.