307294: CF1334E. Divisor Paths
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Divisor Paths
题意翻译
有一个无向带权图,所有的点为 $D$ 的约数,$x,y$ 连边当且仅当存在质数 $p$ 使得 $x\cdot p = y$,边权为 $d(y) - d(x)$,其中 $d$ 为约数个数函数。 $q$ 个询问 $u,v$ 之间的最短路径条数。 $D \le 10^{15}, q \le 3\times 10^5$题目描述
You are given a positive integer $ D $ . Let's build the following graph from it: - each vertex is a divisor of $ D $ (not necessarily prime, $ 1 $ and $ D $ itself are also included); - two vertices $ x $ and $ y $ ( $ x > y $ ) have an undirected edge between them if $ x $ is divisible by $ y $ and $ \frac x y $ is a prime; - the weight of an edge is the number of divisors of $ x $ that are not divisors of $ y $ . For example, here is the graph for $ D=12 $ : 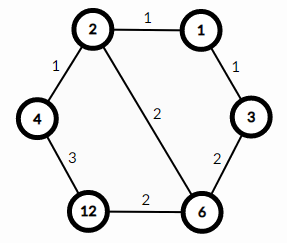Edge $ (4,12) $ has weight $ 3 $ because $ 12 $ has divisors $ [1,2,3,4,6,12] $ and $ 4 $ has divisors $ [1,2,4] $ . Thus, there are $ 3 $ divisors of $ 12 $ that are not divisors of $ 4 $ — $ [3,6,12] $ . There is no edge between $ 3 $ and $ 2 $ because $ 3 $ is not divisible by $ 2 $ . There is no edge between $ 12 $ and $ 3 $ because $ \frac{12}{3}=4 $ is not a prime. Let the length of the path between some vertices $ v $ and $ u $ in the graph be the total weight of edges on it. For example, path $ [(1, 2), (2, 6), (6, 12), (12, 4), (4, 2), (2, 6)] $ has length $ 1+2+2+3+1+2=11 $ . The empty path has length $ 0 $ . So the shortest path between two vertices $ v $ and $ u $ is the path that has the minimal possible length. Two paths $ a $ and $ b $ are different if there is either a different number of edges in them or there is a position $ i $ such that $ a_i $ and $ b_i $ are different edges. You are given $ q $ queries of the following form: - $ v $ $ u $ — calculate the number of the shortest paths between vertices $ v $ and $ u $ . The answer for each query might be large so print it modulo $ 998244353 $ .输入输出格式
输入格式
The first line contains a single integer $ D $ ( $ 1 \le D \le 10^{15} $ ) — the number the graph is built from. The second line contains a single integer $ q $ ( $ 1 \le q \le 3 \cdot 10^5 $ ) — the number of queries. Each of the next $ q $ lines contains two integers $ v $ and $ u $ ( $ 1 \le v, u \le D $ ). It is guaranteed that $ D $ is divisible by both $ v $ and $ u $ (both $ v $ and $ u $ are divisors of $ D $ ).
输出格式
Print $ q $ integers — for each query output the number of the shortest paths between the two given vertices modulo $ 998244353 $ .
输入输出样例
输入样例 #1
12
3
4 4
12 1
3 4输出样例 #1
1
3
1输入样例 #2
1
1
1 1输出样例 #2
1输入样例 #3
288807105787200
4
46 482955026400
12556830686400 897
414 12556830686400
4443186242880 325输出样例 #3
547558588
277147129
457421435
702277623