Numbers on Tree

题意翻译

有一棵形态确定的有根树，结点编号为 $1,\cdots,n$，每个结点 $i$ 有权值 $a_i$。 定义 $c_i$ 表示：满足 $j$ 在 $i$ 子树内且 $a_j<a_i$ 的 $j$ 的个数。 现在给定所有的 $c_i$，请你构造一种 $a_i$ 的方案使得所有 $c_i$ 成立，你构造的方案要满足 $1\leq a_i\leq 10^9$，且 $a_i$ 是整数。 --- 输入中，第一行为表示结点数量的 $n$ $(n\leq 2000)$，之后 $n$ 行中第 $i$ 行两个整数依次为 $p_i$ 和 $c_i$，$p_i$ 表示 $i$ 的父结点，根节点的 $p_i=0$。 若存在一组 $a_i$ 满足方案，第一行输出 ```YES ``` 并在第二行依次输出所有 $a_i$；否则输出一行 ```NO```。

题目描述

Evlampiy was gifted a rooted tree. The vertices of the tree are numbered from $ 1 $ to $ n $ . Each of its vertices also has an integer $ a_i $ written on it. For each vertex $ i $ , Evlampiy calculated $ c_i $ — the number of vertices $ j $ in the subtree of vertex $ i $ , such that $ a_j < a_i $ . 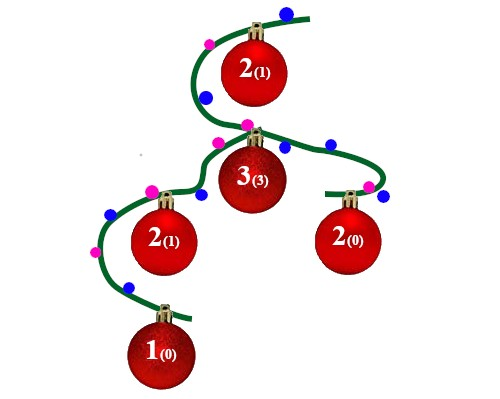Illustration for the second example, the first integer is $ a_i $ and the integer in parentheses is $ c_i $ After the new year, Evlampiy could not remember what his gift was! He remembers the tree and the values of $ c_i $ , but he completely forgot which integers $ a_i $ were written on the vertices. Help him to restore initial integers!

输入输出格式

输入格式

The first line contains an integer $ n $ $ (1 \leq n \leq 2000) $ — the number of vertices in the tree. The next $ n $ lines contain descriptions of vertices: the $ i $ -th line contains two integers $ p_i $ and $ c_i $ ( $ 0 \leq p_i \leq n $ ; $ 0 \leq c_i \leq n-1 $ ), where $ p_i $ is the parent of vertex $ i $ or $ 0 $ if vertex $ i $ is root, and $ c_i $ is the number of vertices $ j $ in the subtree of vertex $ i $ , such that $ a_j < a_i $ . It is guaranteed that the values of $ p_i $ describe a rooted tree with $ n $ vertices.

输出格式

If a solution exists, in the first line print "YES", and in the second line output $ n $ integers $ a_i $ $ (1 \leq a_i \leq {10}^{9}) $ . If there are several solutions, output any of them. One can prove that if there is a solution, then there is also a solution in which all $ a_i $ are between $ 1 $ and $ 10^9 $ . If there are no solutions, print "NO".

输入输出样例

输入样例 #1

3
2 0
0 2
2 0

输出样例 #1

YES
1 2 1

输入样例 #2

5
0 1
1 3
2 1
3 0
2 0

输出样例 #2

YES
2 3 2 1 2