Filling the Grid

题意翻译

有一个h*w的网格 - ri：每一行从左边第一列开始连续的满格子数 - hi：每一列从上面第一格开始连续的满格子数 一开始网格全为空，找到有多少种方法（mod 1000000007），使得网格的状态满足ri和hi。

题目描述

Suppose there is a $ h \times w $ grid consisting of empty or full cells. Let's make some definitions: - $ r_{i} $ is the number of consecutive full cells connected to the left side in the $ i $ -th row ( $ 1 \le i \le h $ ). In particular, $ r_i=0 $ if the leftmost cell of the $ i $ -th row is empty. - $ c_{j} $ is the number of consecutive full cells connected to the top end in the $ j $ -th column ( $ 1 \le j \le w $ ). In particular, $ c_j=0 $ if the topmost cell of the $ j $ -th column is empty. In other words, the $ i $ -th row starts exactly with $ r_i $ full cells. Similarly, the $ j $ -th column starts exactly with $ c_j $ full cells. 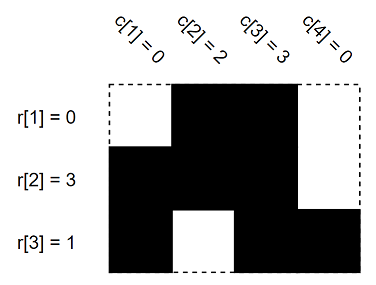These are the $ r $ and $ c $ values of some $ 3 \times 4 $ grid. Black cells are full and white cells are empty.You have values of $ r $ and $ c $ . Initially, all cells are empty. Find the number of ways to fill grid cells to satisfy values of $ r $ and $ c $ . Since the answer can be very large, find the answer modulo $ 1000000007\,(10^{9} + 7) $ . In other words, find the remainder after division of the answer by $ 1000000007\,(10^{9} + 7) $ .

输入输出格式

输入格式

The first line contains two integers $ h $ and $ w $ ( $ 1 \le h, w \le 10^{3} $ ) — the height and width of the grid. The second line contains $ h $ integers $ r_{1}, r_{2}, \ldots, r_{h} $ ( $ 0 \le r_{i} \le w $ ) — the values of $ r $ . The third line contains $ w $ integers $ c_{1}, c_{2}, \ldots, c_{w} $ ( $ 0 \le c_{j} \le h $ ) — the values of $ c $ .

输出格式

Print the answer modulo $ 1000000007\,(10^{9} + 7) $ .

输入输出样例

输入样例 #1

3 4
0 3 1
0 2 3 0

输出样例 #1

2

输入样例 #2

1 1
0
1

输出样例 #2

0

输入样例 #3

19 16
16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12
6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4

输出样例 #3

797922655

说明

In the first example, this is the other possible case. In the second example, it's impossible to make a grid to satisfy such $ r $ , $ c $ values. In the third example, make sure to print answer modulo $ (10^9 + 7) $ .