306515: CF1209B. Koala and Lights
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Koala and Lights
题意翻译
有 $n$ 盏灯泡,给定初始状态,第 $i$ 盏灯泡会在 $b_i,b_i+a_i,b_i+2 \times a_i$ 等时刻变成相反的状态,求在某一个时刻亮灯数的最大值。 **【输入格式】** 第一行包含一个整数 $n$ ($1 \leq n \leq 100$),表示有 $n$ 盏灯。 下一行包含一个 $n$ 个元素的字符串 $s$,如果 $s_i$ 为 $\verb!1!$,表示第 $i$ 盏灯初始是亮起的; 如果 $s_i$ 为 $\verb!0!$ ,表示第 $i$ 盏灯初始是熄灭的。 接下来 $n$ 行,每行包含两个整数 $a_i$ 和 $b_i$。 **【输出格式】** 一行,表示在某一时刻亮灯数的最大值。题目描述
It is a holiday season, and Koala is decorating his house with cool lights! He owns $ n $ lights, all of which flash periodically. After taking a quick glance at them, Koala realizes that each of his lights can be described with two parameters $ a_i $ and $ b_i $ . Light with parameters $ a_i $ and $ b_i $ will toggle (on to off, or off to on) every $ a_i $ seconds starting from the $ b_i $ -th second. In other words, it will toggle at the moments $ b_i $ , $ b_i + a_i $ , $ b_i + 2 \cdot a_i $ and so on. You know for each light whether it's initially on or off and its corresponding parameters $ a_i $ and $ b_i $ . Koala is wondering what is the maximum number of lights that will ever be on at the same time. So you need to find that out. 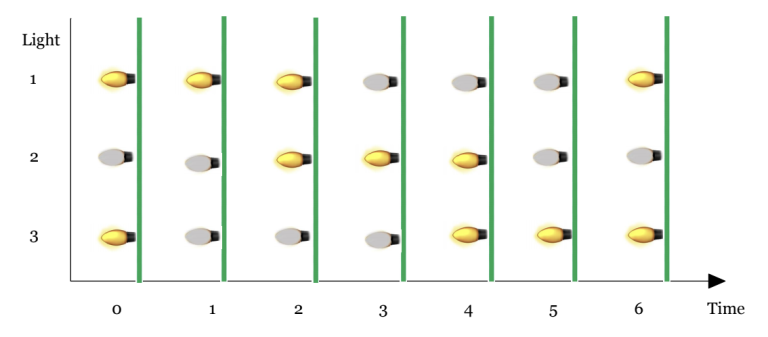Here is a graphic for the first example.输入输出格式
输入格式
The first line contains a single integer $ n $ ( $ 1 \le n \le 100 $ ), the number of lights. The next line contains a string $ s $ of $ n $ characters. The $ i $ -th character is "1", if the $ i $ -th lamp is initially on. Otherwise, $ i $ -th character is "0". The $ i $ -th of the following $ n $ lines contains two integers $ a_i $ and $ b_i $ ( $ 1 \le a_i, b_i \le 5 $ ) — the parameters of the $ i $ -th light.
输出格式
Print a single integer — the maximum number of lights that will ever be on at the same time.
输入输出样例
输入样例 #1
3
101
3 3
3 2
3 1
输出样例 #1
2
输入样例 #2
4
1111
3 4
5 2
3 1
3 2
输出样例 #2
4
输入样例 #3
6
011100
5 3
5 5
2 4
3 5
4 2
1 5
输出样例 #3
6