Almost Equal

题意翻译

### Problem C Almost Equal 题意：给出一个数字n，由1,2,3,...,2*n按一定顺序组成一个圆环，求出一种顺序使得以下成立： 将圆环上的每n个连续数字累加起来得到一个和，将这个和写在黑板上，写完2n个和以后，使得黑板上任意两个和的差小于等于1。 举例： 当n=3的情况：  在左图中，1+4+5=10,4+5+2=11,5+2+3=10,2+3+6=11,3+6+1=10,6+1+4=11 |11-10|<=1,满足题意。 在右图中，1+5+6=12,3+2+4=9, |12-9|>=3,不满足题意。 输入：一个正整数n,(1<=n<=100000) 输出：如果没有解决方案，输出“NO” ​ 如果有解决方案，输出“YES”，下一行输出2n个正整数，表示满足题意的任意一种顺序

题目描述

You are given integer $ n $ . You have to arrange numbers from $ 1 $ to $ 2n $ , using each of them exactly once, on the circle, so that the following condition would be satisfied: For every $ n $ consecutive numbers on the circle write their sum on the blackboard. Then any two of written on the blackboard $ 2n $ numbers differ not more than by $ 1 $ . For example, choose $ n = 3 $ . On the left you can see an example of a valid arrangement: $ 1 + 4 + 5 = 10 $ , $ 4 + 5 + 2 = 11 $ , $ 5 + 2 + 3 = 10 $ , $ 2 + 3 + 6 = 11 $ , $ 3 + 6 + 1 = 10 $ , $ 6 + 1 + 4 = 11 $ , any two numbers differ by at most $ 1 $ . On the right you can see an invalid arrangement: for example, $ 5 + 1 + 6 = 12 $ , and $ 3 + 2 + 4 = 9 $ , $ 9 $ and $ 12 $ differ more than by $ 1 $ .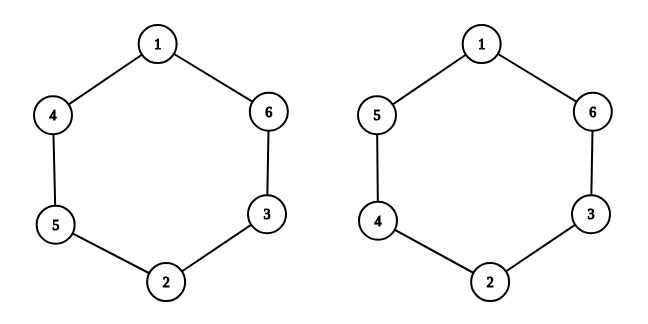 

输入输出格式

输入格式

The first and the only line contain one integer $ n $ ( $ 1 \le n \le 10^5 $ ).

输出格式

If there is no solution, output "NO" in the first line. If there is a solution, output "YES" in the first line. In the second line output $ 2n $ numbers — numbers from $ 1 $ to $ 2n $ in the order they will stay in the circle. Each number should appear only once. If there are several solutions, you can output any of them.

输入输出样例

输入样例 #1

3

输出样例 #1

YES
1 4 5 2 3 6 

输入样例 #2

4

输出样例 #2

NO

说明

Example from the statement is shown for the first example. It can be proved that there is no solution in the second example.