Low Budget Inception

题意翻译

## 题目描述 我们渐感无趣，并打算猜测在超低预算下，影片会如何进行「开头」的制作。 我们仍记得的第一个场景中，整个城市都扭曲了：  它或许需要很高的 CGI 费用，但幸运地，我们有另一个类似的廉价方案。 首先，忘却一切的 3D，那些只是土豪的玩具！ 现在，城市以一条数轴表示。 第二，这个城市没有必要符合常理。 数轴上有 $n$ 个建筑物，建筑物都可以视作 $1 \times 1$ 的正方形。 **建筑物按其位置的升序，依次编号为 $1,\dots,n$。** 第 $i$ 个建筑物的左下角和右下角分别位于 $a_i$ 和 $a_i + 1$ 处。 并且，保证相邻建筑物的距离不超过 $d$（单纯为了让城市看上去不那么稀疏）。 其中第 $i$ 个和第 $i + 1$ 个建筑物的距离为前者的右下角和后者的左下角的距离。 最后，曲率也非常难以复现。 我们使用如下算法来处理整点 $x$ 处的弯曲： 令一条从 $x$ 向 $+\infty$ 延伸的射线及其经过的所有建筑物绕点 $x$ 开始逆时针转动。直到某个角度，一些建筑物将会触及其他建筑物或者数轴的一部分。 这个角度就是弯曲的结果。 （建筑物被破坏也不会花费额外经费） **最终状态下，我们称两条射线之间的角度为最终角度 $\alpha_x$。** 最后的问题在于寻找最佳的 $x$ 并进行弯曲。幸运的是，我们已经有了 $m$ 个候选点。 于是，你的任务是帮助我们对于候选点中的所有 $x$，计算所有的最终角度 $\alpha_x$。 ## 输入输出格式 **输入格式：** 第一行，两个整数 $n,d\;(1 \le n \le 2 \cdot 10^5,0 \le d \le 7000)$，表示建筑物的个数和相邻建筑物的最大距离。 第二行，$n$ 个整数 $a_1,\dots,a_n\;(a_1 = 0,0 < a_{i + 1} - a_i \le d + 1)$，表示建筑物的坐标。 第三行，一个整数 $m\;(1 \le m \le 2 \cdot 10^5)$，表示候选点的个数。 第四行，$m$ 个整数 $x_1,\dots,x_m\;(0 \le x_i \le a_n + 1,x_i < x_{i + 1})$，表示候选点的坐标。 **输出格式：** 对于每个 $x_i$，输出 $\alpha_{x_i}$（以弧度表示）。 误差不超过 $10^{-9}$。 ## 说明 你可以在此看见第一个样例中的城市和 $2$ 处的弯曲。你需要测量的角度已经被标记为蓝色。它等于 $\frac \pi 4$。 没有任何一对建筑物的距离超过 $4$，所以当 $d = 4$ 时也合法。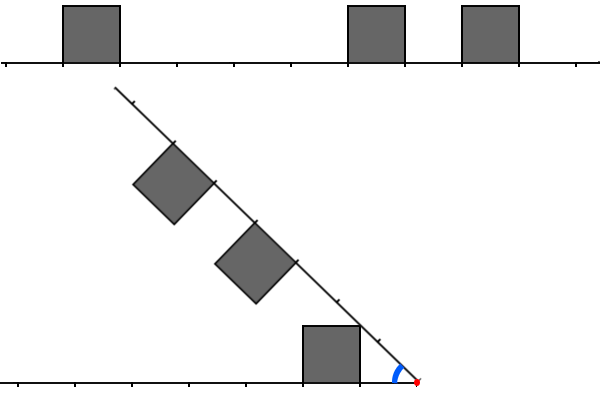 

题目描述

So we got bored and decided to take our own guess at how would "Inception" production go if the budget for the film had been terribly low. The first scene we remembered was the one that features the whole city bending onto itself: It feels like it will require high CGI expenses, doesn't it? Luckily, we came up with a similar-looking scene which was a tiny bit cheaper to make. Firstly, forget about 3D, that's hard and expensive! The city is now represented as a number line (infinite to make it easier, of course). Secondly, the city doesn't have to look natural at all. There are $ n $ buildings on the line. Each building is a square $ 1 \times 1 $ . Buildings are numbered from $ 1 $ to $ n $ in ascending order of their positions. Lower corners of building $ i $ are at integer points $ a_i $ and $ a_i + 1 $ of the number line. Also the distance between any two neighbouring buildings $ i $ and $ i + 1 $ doesn't exceed $ d $ (really, this condition is here just to make the city look not that sparse). Distance between some neighbouring buildings $ i $ and $ i + 1 $ is calculated from the lower right corner of building $ i $ to the lower left corner of building $ i + 1 $ . Finally, curvature of the bend is also really hard to simulate! Let the bend at some integer coordinate $ x $ be performed with the following algorithm. Take the ray from $ x $ to $ +\infty $ and all the buildings which are on this ray and start turning the ray and the buildings counter-clockwise around point $ x $ . At some angle some building will touch either another building or a part of the line. You have to stop bending there (implementing buildings crushing is also not worth its money). Let's call the angle between two rays in the final state the terminal angle $ \alpha_x $ . The only thing left is to decide what integer point $ x $ is the best to start bending around. Fortunately, we've already chosen $ m $ candidates to perform the bending. So, can you please help us to calculate terminal angle $ \alpha_x $ for each bend $ x $ from our list of candidates?

输入输出格式

输入格式

The first line contains two integer numbers $ n $ and $ d $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le d \le 7000 $ ) — the number of buildings and the maximum distance between any pair of neighbouring buildings, respectively. The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ a_1 = 0 $ , $ 0 < a_{i + 1} - a_i \le d + 1 $ ) — coordinates of left corners of corresponding buildings in ascending order. The third line contains single integer $ m $ ( $ 1 \le m \le 2 \cdot 10^5 $ ) — the number of candidates. The fourth line contains $ m $ integers $ x_1, x_2, \dots, x_m $ ( $ 0 \le x_i \le a_n + 1 $ , $ x_i < x_{i + 1} $ ) — the coordinates of bends you need to calculate terminal angles for in ascending order.

输出格式

Print $ m $ numbers. For each bend $ x_i $ print terminal angle $ \alpha_{x_i} $ (in radians). Your answer is considered correct if its absolute error does not exceed $ 10^{-9} $ . Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer is accepted if and only if $ |a - b| \le 10^{-9} $ .

输入输出样例

输入样例 #1

3 5
0 5 7
9
0 1 2 3 4 5 6 7 8

输出样例 #1

1.570796326794897
1.570796326794897
0.785398163397448
0.927295218001612
0.785398163397448
1.570796326794897
1.570796326794897
1.570796326794897
1.570796326794897

输入样例 #2

2 7
0 4
3
1 3 4

输出样例 #2

1.570796326794897
0.927295218001612
1.570796326794897

输入样例 #3

5 0
0 1 2 3 4
6
0 1 2 3 4 5

输出样例 #3

1.570796326794897
3.141592653589793
3.141592653589793
3.141592653589793
3.141592653589793
1.570796326794897

说明

Here you can see the picture of the city for the first example and the bend at position $ 2 $ for it. The angle you need to measure is marked blue. You can see that it's equal to $ \frac \pi 4 $ . You can see that no pair of neighbouring buildings have distance more than $ 4 $ between them. $ d = 4 $ would also suffice for that test. 

题意翻译

## 题目描述 我们渐感无趣，并打算猜测在超低预算下，影片会如何进行「开头」的制作。 我们仍记得的第一个场景中，整个城市都扭曲了：  它或许需要很高的 CGI 费用，但幸运地，我们有另一个类似的廉价方案。 首先，忘却一切的 3D，那些只是土豪的玩具！ 现在，城市以一条数轴表示。 第二，这个城市没有必要符合常理。 数轴上有 $n$ 个建筑物，建筑物都可以视作 $1 \times 1$ 的正方形。 **建筑物按其位置的升序，依次编号为 $1,\dots,n$。** 第 $i$ 个建筑物的左下角和右下角分别位于 $a_i$ 和 $a_i + 1$ 处。 并且，保证相邻建筑物的距离不超过 $d$（单纯为了让城市看上去不那么稀疏）。 其中第 $i$ 个和第 $i + 1$ 个建筑物的距离为前者的右下角和后者的左下角的距离。 最后，曲率也非常难以复现。 我们使用如下算法来处理整点 $x$ 处的弯曲： 令一条从 $x$ 向 $+\infty$ 延伸的射线及其经过的所有建筑物绕点 $x$ 开始逆时针转动。直到某个角度，一些建筑物将会触及其他建筑物或者数轴的一部分。 这个角度就是弯曲的结果。 （建筑物被破坏也不会花费额外经费） **最终状态下，我们称两条射线之间的角度为最终角度 $\alpha_x$。** 最后的问题在于寻找最佳的 $x$ 并进行弯曲。幸运的是，我们已经有了 $m$ 个候选点。 于是，你的任务是帮助我们对于候选点中的所有 $x$，计算所有的最终角度 $\alpha_x$。 ## 输入输出格式 **输入格式：** 第一行，两个整数 $n,d\;(1 \le n \le 2 \cdot 10^5,0 \le d \le 7000)$，表示建筑物的个数和相邻建筑物的最大距离。 第二行，$n$ 个整数 $a_1,\dots,a_n\;(a_1 = 0,0 < a_{i + 1} - a_i \le d + 1)$，表示建筑物的坐标。 第三行，一个整数 $m\;(1 \le m \le 2 \cdot 10^5)$，表示候选点的个数。 第四行，$m$ 个整数 $x_1,\dots,x_m\;(0 \le x_i \le a_n + 1,x_i < x_{i + 1})$，表示候选点的坐标。 **输出格式：** 对于每个 $x_i$，输出 $\alpha_{x_i}$（以弧度表示）。 误差不超过 $10^{-9}$。 ## 说明 你可以在此看见第一个样例中的城市和 $2$ 处的弯曲。你需要测量的角度已经被标记为蓝色。它等于 $\frac \pi 4$。 没有任何一对建筑物的距离超过 $4$，所以当 $d = 4$ 时也合法。