Multicolored Markers

题意翻译

题目大意:给定两个数$a,b(1\leq a,b\leq 10^{14})$分别表示红色方格个数和蓝色方格个数,求这$a$个红色方格和$b$个蓝色方格构成的矩形周长的最小值,且满足在所构成的矩形中至少有一种颜色的所有方块也能构成一个矩形,数据保证存在至少一种合法的染色方案.

题目描述

There is an infinite board of square tiles. Initially all tiles are white. Vova has a red marker and a blue marker. Red marker can color $ a $ tiles. Blue marker can color $ b $ tiles. If some tile isn't white then you can't use marker of any color on it. Each marker must be drained completely, so at the end there should be exactly $ a $ red tiles and exactly $ b $ blue tiles across the board. Vova wants to color such a set of tiles that: - they would form a rectangle, consisting of exactly $ a+b $ colored tiles; - all tiles of at least one color would also form a rectangle. Here are some examples of correct colorings: 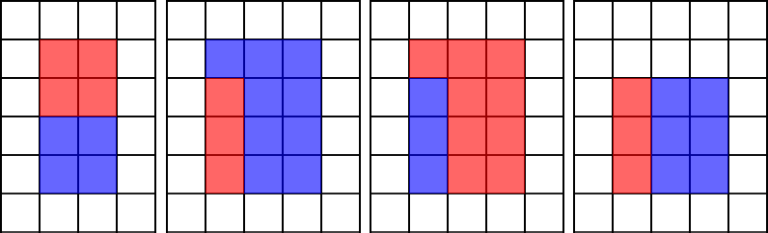Here are some examples of incorrect colorings: 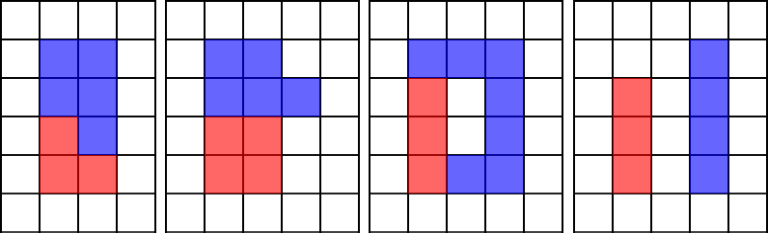Among all correct colorings Vova wants to choose the one with the minimal perimeter. What is the minimal perimeter Vova can obtain? It is guaranteed that there exists at least one correct coloring.

输入输出格式

输入格式

A single line contains two integers $ a $ and $ b $ ( $ 1 \le a, b \le 10^{14} $ ) — the number of tiles red marker should color and the number of tiles blue marker should color, respectively.

输出格式

Print a single integer — the minimal perimeter of a colored rectangle Vova can obtain by coloring exactly $ a $ tiles red and exactly $ b $ tiles blue. It is guaranteed that there exists at least one correct coloring.

输入输出样例

输入样例 #1

4 4

输出样例 #1

12

输入样例 #2

3 9

输出样例 #2

14

输入样例 #3

9 3

输出样例 #3

14

输入样例 #4

3 6

输出样例 #4

12

输入样例 #5

506 2708

输出样例 #5

3218

说明

The first four examples correspond to the first picture of the statement. Note that for there exist multiple correct colorings for all of the examples. In the first example you can also make a rectangle with sides $ 1 $ and $ 8 $ , though its perimeter will be $ 18 $ which is greater than $ 8 $ . In the second example you can make the same resulting rectangle with sides $ 3 $ and $ 4 $ , but red tiles will form the rectangle with sides $ 1 $ and $ 3 $ and blue tiles will form the rectangle with sides $ 3 $ and $ 3 $ .

题意翻译

题目大意:给定两个数$a,b(1\leq a,b\leq 10^{14})$分别表示红色方格个数和蓝色方格个数,求这$a$个红色方格和$b$个蓝色方格构成的矩形周长的最小值,且满足在所构成的矩形中至少有一种颜色的所有方块也能构成一个矩形,数据保证存在至少一种合法的染色方案.