Numbers on the Chessboard

题意翻译

## 题目描述 你有一个 **n×n** 的棋盘，这个棋盘中的数字是由 **1** 至 **n×n** 的数组成的。这些数的填法满足： 前面的 **⌈n×n/2⌉** 个数字，即 **1** 至 **⌈n×n/2⌉** ，被按照从左到右、从上到下的次序依次写在那些横纵坐标相加为偶数的格子里。 剩下的 **n×n-⌈n×n/2⌉** 个数，即 **⌈n×n/2⌉+1** 至 **n×n** ，也被按照如上顺序依次写在那些横纵坐标相加为奇数的格子里。 这里的 **⌈y/x⌉** 代表y除以x**向上**取整 你被给到了q个询问，第i个询问是形如xi，yi的。你要对应输出的是在坐标为xi,yi的格子里的数字（xi为行，yi为列），行和列的大小都是从 **1** 至 **n** 。 ## 输入输出格式 ### 输入格式： 第一行包含了两个整数n和q（1≤n≤1e9，1≤q≤1e5),分别代表板的大小和询问的次数 接下来的q行都给出了xi与yi，代表第i次询问 ### 输出格式： 对于1至q的每一次询问，输出在坐标为xi,yi的格子里的数字（注意要换行

题目描述

You are given a chessboard of size $ n \times n $ . It is filled with numbers from $ 1 $ to $ n^2 $ in the following way: the first $ \lceil \frac{n^2}{2} \rceil $ numbers from $ 1 $ to $ \lceil \frac{n^2}{2} \rceil $ are written in the cells with even sum of coordinates from left to right from top to bottom. The rest $ n^2 - \lceil \frac{n^2}{2} \rceil $ numbers from $ \lceil \frac{n^2}{2} \rceil + 1 $ to $ n^2 $ are written in the cells with odd sum of coordinates from left to right from top to bottom. The operation $ \lceil\frac{x}{y}\rceil $ means division $ x $ by $ y $ rounded up. For example, the left board on the following picture is the chessboard which is given for $ n=4 $ and the right board is the chessboard which is given for $ n=5 $ . 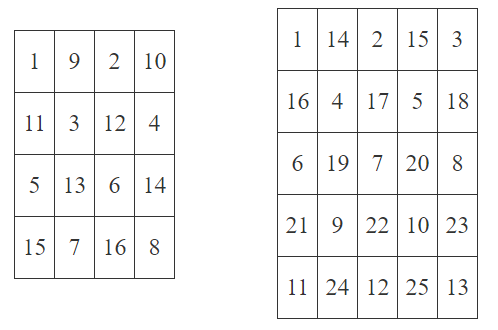You are given $ q $ queries. The $ i $ -th query is described as a pair $ x_i, y_i $ . The answer to the $ i $ -th query is the number written in the cell $ x_i, y_i $ ( $ x_i $ is the row, $ y_i $ is the column). Rows and columns are numbered from $ 1 $ to $ n $ .

输入输出格式

输入格式

The first line contains two integers $ n $ and $ q $ ( $ 1 \le n \le 10^9 $ , $ 1 \le q \le 10^5 $ ) — the size of the board and the number of queries. The next $ q $ lines contain two integers each. The $ i $ -th line contains two integers $ x_i, y_i $ ( $ 1 \le x_i, y_i \le n $ ) — description of the $ i $ -th query.

输出格式

For each query from $ 1 $ to $ q $ print the answer to this query. The answer to the $ i $ -th query is the number written in the cell $ x_i, y_i $ ( $ x_i $ is the row, $ y_i $ is the column). Rows and columns are numbered from $ 1 $ to $ n $ . Queries are numbered from $ 1 $ to $ q $ in order of the input.

输入输出样例

输入样例 #1

4 5
1 1
4 4
4 3
3 2
2 4

输出样例 #1

1
8
16
13
4

输入样例 #2

5 4
2 1
4 2
3 3
3 4

输出样例 #2

16
9
7
20

说明

Answers to the queries from examples are on the board in the picture from the problem statement.