Reachability from the Capital

题意翻译

## 题目描述 在 Berland 有 $n$ 座城市和 $m$ 条道路，每条道路连接着一对城市。 Berland 的道路都是**单向**的 为了能让首都能够到达所有的城市，最少需要新修建多少新道路？ 新道路也是单向的 ## 输入格式 输入的第一行包含三个整数 $n,m$ 和 $s$ $(1\le n \le 5000,0\le m \le 5000 , 1\le s \le n)$ ——城市数，道路数和首都所在城市的标号。 城市的标号为 $1$ \~ $n$ 接下来 $m$ 行每行包含一条道路连接着一对城市 $u_i,v_i$ $(1\le u_i,v_i\le n,u_i\ne v_i)$ 对于每对城市 $u,v$，从 $u$ 到 $v$ 最多只能有一条道路。 允许在一对城市之间建造相反方向的道路（即从 $u$ 到 $v$ 和从 $v$ 到 $u$ ）。 ## 输出格式 输出一个整数——使从首都可以到达所有城市所需的最少新修建道路数。如果从 $s$ 已经可以到达所有城市，则输出 $0$。 ## 说明/提示 样例 1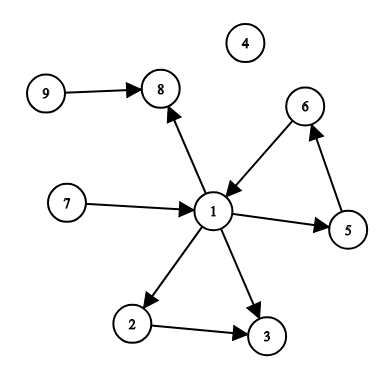：  例如，您可以添加道路 ( 6, 4 ) , ( 7 , 9 ) , ( 1 , 7 )，以使从 $s = 1$ 可到达所有城市。 样例 2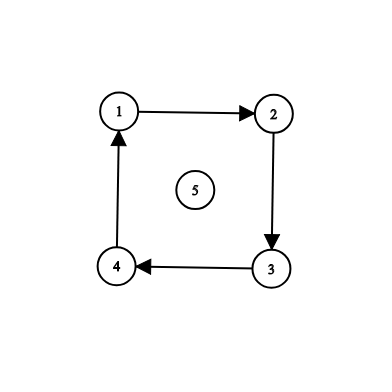：  在此样例中，您可以添加道路（5 , 1），（5 , 2），（5 , 3），（5 , 4）中的任何一条，以使可从 $s = 5$ 到达所有城市。

题目描述

There are $ n $ cities and $ m $ roads in Berland. Each road connects a pair of cities. The roads in Berland are one-way. What is the minimum number of new roads that need to be built to make all the cities reachable from the capital? New roads will also be one-way.

输入输出格式

输入格式

The first line of input consists of three integers $ n $ , $ m $ and $ s $ ( $ 1 \le n \le 5000, 0 \le m \le 5000, 1 \le s \le n $ ) — the number of cities, the number of roads and the index of the capital. Cities are indexed from $ 1 $ to $ n $ . The following $ m $ lines contain roads: road $ i $ is given as a pair of cities $ u_i $ , $ v_i $ ( $ 1 \le u_i, v_i \le n $ , $ u_i \ne v_i $ ). For each pair of cities $ (u, v) $ , there can be at most one road from $ u $ to $ v $ . Roads in opposite directions between a pair of cities are allowed (i.e. from $ u $ to $ v $ and from $ v $ to $ u $ ).

输出格式

Print one integer — the minimum number of extra roads needed to make all the cities reachable from city $ s $ . If all the cities are already reachable from $ s $ , print 0.

输入输出样例

输入样例 #1

9 9 1
1 2
1 3
2 3
1 5
5 6
6 1
1 8
9 8
7 1

输出样例 #1

3

输入样例 #2

5 4 5
1 2
2 3
3 4
4 1

输出样例 #2

1

说明

The first example is illustrated by the following: For example, you can add roads ( $ 6, 4 $ ), ( $ 7, 9 $ ), ( $ 1, 7 $ ) to make all the cities reachable from $ s = 1 $ . The second example is illustrated by the following: In this example, you can add any one of the roads ( $ 5, 1 $ ), ( $ 5, 2 $ ), ( $ 5, 3 $ ), ( $ 5, 4 $ ) to make all the cities reachable from $ s = 5 $ .