Water Taps

题意翻译

∀xi∈[1,ai],对于所有满足∑xi(ti−T)=0的情况,求∑xi的最大值，若不存在解，则输出0

题目描述

Consider a system of $ n $ water taps all pouring water into the same container. The $ i $ -th water tap can be set to deliver any amount of water from $ 0 $ to $ a_{i} $ ml per second (this amount may be a real number). The water delivered by $ i $ -th tap has temperature $ t_{i} $ . If for every 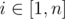 you set $ i $ -th tap to deliver exactly $ x_{i} $ ml of water per second, then the resulting temperature of water will be 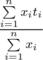 (if 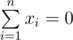, then to avoid division by zero we state that the resulting water temperature is $ 0 $ ). You have to set all the water taps in such a way that the resulting temperature is exactly $ T $ . What is the maximum amount of water you may get per second if its temperature has to be $ T $ ?

输入输出格式

输入格式

The first line contains two integers $ n $ and $ T $ ( $ 1<=n<=200000 $ , $ 1<=T<=10^{6} $ ) — the number of water taps and the desired temperature of water, respectively. The second line contains $ n $ integers $ a_{1} $ , $ a_{2} $ , ..., $ a_{n} $ ( $ 1<=a_{i}<=10^{6} $ ) where $ a_{i} $ is the maximum amount of water $ i $ -th tap can deliver per second. The third line contains $ n $ integers $ t_{1} $ , $ t_{2} $ , ..., $ t_{n} $ ( $ 1<=t_{i}<=10^{6} $ ) — the temperature of water each tap delivers.

输出格式

Print the maximum possible amount of water with temperature exactly $ T $ you can get per second (if it is impossible to obtain water with such temperature, then the answer is considered to be $ 0 $ ). Your answer is considered correct if its absolute or relative error doesn't exceed $ 10^{-6} $ .

输入输出样例

输入样例 #1

2 100
3 10
50 150

输出样例 #1

6.000000000000000

输入样例 #2

3 9
5 5 30
6 6 10

输出样例 #2

40.000000000000000

输入样例 #3

2 12
1 3
10 15

输出样例 #3

1.666666666666667