Constructing Tests

题意翻译

给定两个正整数n,m(m≤n)，对于一个n阶0-1方阵， 其任意m阶子方阵中至少有一个元素“0”，则可以求解这个方阵中的“1”的最大数目。现求解这个问题的逆向问题：已知这个最大数目为X，求相应的n和m。

题目描述

Let's denote a $ m $ -free matrix as a binary (that is, consisting of only $ 1 $ 's and $ 0 $ 's) matrix such that every square submatrix of size $ m×m $ of this matrix contains at least one zero. Consider the following problem: You are given two integers $ n $ and $ m $ . You have to construct an $ m $ -free square matrix of size $ n×n $ such that the number of $ 1 $ 's in this matrix is maximum possible. Print the maximum possible number of $ 1 $ 's in such matrix. You don't have to solve this problem. Instead, you have to construct a few tests for it. You will be given $ t $ numbers $ x_{1} $ , $ x_{2} $ , ..., $ x_{t} $ . For every 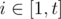, find two integers $ n_{i} $ and $ m_{i} $ ( $ n_{i}>=m_{i} $ ) such that the answer for the aforementioned problem is exactly $ x_{i} $ if we set $ n=n_{i} $ and $ m=m_{i} $ .

输入输出格式

输入格式

The first line contains one integer $ t $ ( $ 1<=t<=100 $ ) — the number of tests you have to construct. Then $ t $ lines follow, $ i $ -th line containing one integer $ x_{i} $ ( $ 0<=x_{i}<=10^{9} $ ). Note that in hacks you have to set $ t=1 $ .

输出格式

For each test you have to construct, output two positive numbers $ n_{i} $ and $ m_{i} $ ( $ 1<=m_{i}<=n_{i}<=10^{9} $ ) such that the maximum number of $ 1 $ 's in a $ m_{i} $ -free $ n_{i}×n_{i} $ matrix is exactly $ x_{i} $ . If there are multiple solutions, you may output any of them; and if this is impossible to construct a test, output a single integer $ -1 $ .

输入输出样例

输入样例 #1

3
21
0
1

输出样例 #1

5 2
1 1
-1