A Game With Numbers

题意翻译

想象Alice正在和Bob玩纸牌游戏，两个人都正好有8张牌，每张卡片上都有一个整数，整数范围为0~4。每一回合，Alice或Bob轮流从不同的卡片中选择两张牌，两张牌分别为A和B，A是自己的牌，B是对方的牌（A乘B不等于0）。另一个数C=（A+B） mod 5，然后用C代替A，然后一直反复计算C，直到某人八张卡片均变为0后，他就赢了。 现在Alice想知道每一局谁会赢，她会告诉你每人的牌，和第一个拿牌的人，你的任务是算出谁会赢（没有傻瓜式操作） 感谢@风格雨关 提供的翻译

题目描述

Imagine that Alice is playing a card game with her friend Bob. They both have exactly $ 8 $ cards and there is an integer on each card, ranging from $ 0 $ to $ 4 $ . In each round, Alice or Bob in turns choose two cards from different players, let them be $ a $ and $ b $ , where $ a $ is the number on the player's card, and $ b $ is the number on the opponent's card. It is necessary that $ a·b≠0 $ . Then they calculate 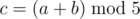 and replace the number $ a $ with $ c $ . The player who ends up with numbers on all $ 8 $ cards being $ 0 $ , wins. Now Alice wants to know who wins in some situations. She will give you her cards' numbers, Bob's cards' numbers and the person playing the first round. Your task is to determine who wins if both of them choose the best operation in their rounds.

输入输出格式

输入格式

The first line contains one positive integer $ T $ ( $ 1<=T<=100000 $ ), denoting the number of situations you need to consider. The following lines describe those $ T $ situations. For each situation: - The first line contains a non-negative integer $ f $ ( $ 0<=f<=1 $ ), where $ f=0 $ means that Alice plays first and $ f=1 $ means Bob plays first. - The second line contains $ 8 $ non-negative integers $ a_{1},a_{2},...,a_{8} $ ( $ 0<=a_{i}<=4 $ ), describing Alice's cards. - The third line contains $ 8 $ non-negative integers $ b_{1},b_{2},...,b_{8} $ ( $ 0<=b_{i}<=4 $ ), describing Bob's cards. We guarantee that if $ f=0 $ , we have 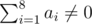. Also when $ f=1 $ , 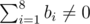 holds.

输出格式

Output $ T $ lines. For each situation, determine who wins. Output - "Alice" (without quotes) if Alice wins. - "Bob" (without quotes) if Bob wins. - "Deal" (without quotes) if it gets into a deal, i.e. no one wins.

输入输出样例

输入样例 #1

4
1
0 0 0 0 0 0 0 0
1 2 3 4 1 2 3 4
1
0 0 0 1 0 0 0 0
0 0 0 0 4 0 0 0
0
1 0 0 0 0 0 0 0
0 0 0 4 0 0 2 0
1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1

输出样例 #1

Alice
Bob
Alice
Deal

说明

In the first situation, Alice has all her numbers $ 0 $ . So she wins immediately. In the second situation, Bob picks the numbers $ 4 $ and $ 1 $ . Because we have , Bob wins after this operation. In the third situation, Alice picks the numbers $ 1 $ and $ 4 $ . She wins after this operation. In the fourth situation, we can prove that it falls into a loop.